Semantic Uncertainty: Linguistic Invariances for Uncertainty Estimation in Natural Language Generation

📄 논문 정보

“Semantic Uncertainty: Linguistic Invariances for Uncertainty Estimation in Natural Language Generation” (ICLR 2023)

🔍 연구 배경 및 문제의식

AI라는 개념이 우리에게 본격적으로 다가온 것은 아마도 알파고의 등장이 계기였을 것이다. 불과 몇 년 전만 해도 멀게만 느껴졌던 기술이 이제는 ChatGPT나 Gemini와 같은 언어 모델의 형태로 우리의 일상 속 깊숙이 자리 잡고 있다. 우리는 자연스럽게 AI에게 질문을 던지고, 복잡한 글쓰기를 부탁하며, 때로는 번역이나 요약까지도 맡긴다. 이처럼 자연어 생성(Natural Language Generation, NLG)이 널리 활용되면서, 한 가지 중요한 질문이 떠오른다. “언어 모델이 내놓는 대답을 우리는 얼마나 신뢰할 수 있는가?” 단지 문장을 생성했다는 이유만으로 그 답이 옳다고 보아도 될까? 혹은 표현이 익숙하지 않다면, 그것은 틀린 답변일까?

기존의 딥러닝 모델들은 이미지 분류나 숫자 예측처럼 명확한 정답이 있는 문제에서 예측의 신뢰도를 확률 분포나 엔트로피를 통해 정량적으로 측정해왔다. 하지만 자연어는 다르다. 하나의 질문에 대해 동일한 의미를 가진 다양한 표현들이 존재할 수 있기 때문이다. 같은 의미를 여러 방식으로 표현할 수 있는 언어의 특성은, 기존의 확률 기반 불확실성 측정 방식으로는 포착되기 어렵다. 예를 들어 언어 모델이 같은 질문에 대해 “서울입니다” 또는 “대한민국의 수도는 서울이예요”라고 답할 수 있다. 우리는 이 두 문장이 동일한 의미를 갖는다는 것을 쉽게 이해하지만, 기존의 언어 모델은 표현의 차이를 근거로 서로 다른 결과로 간주하고, 불필요하게 높은 불확실성을 계산해낸다. 이는 결국 모델의 신뢰도를 왜곡시키고, 실제보다 불안정해 보이게 만들 수 있다.

이 논문은 이러한 문제상황에서 출발한다. 저자들은 자연어의 본질인 “의미”에 주목하여, 문장 단위가 아닌 의미 단위로 확률을 재구성하는 새로운 불확실성 지표인 Semantic Entropy를 제안한다. 핵심 아이디어는 단순하다. 같은 의미를 가진 표현은 하나로 묶고, 그 집합에 대해 엔트로피를 계산한다는 것이다. 이를 통해 모델이 실제로 얼마나 다양한 의미를 동시에 고려하고 있는지를 보다 정확히 파악할 수 있다. 무엇보다도 이 방법은 비지도 방식, Unsupervised learning 방식으로 동작하며, 별도의 추가 학습이나 모델 구조 변경 없이도 기존의 대형 언어 모델에 그대로 적용 가능하다는 점에서 실용성과 확장성이 높다는 장점이 있다. 그럼 지금부터 어떤 문제상황이 있는지, 그리고 방법론 및 실험결과를 자세히 살펴보도록 하겠다.

기존 불확실성 측정의 한계

그렇다면 우선, 기존의 언어 모델들은 불확실성(uncertainty)을 어떤 방식으로 측정해왔을까? 기존 딥러닝에서는 출력에 대한 확신의 정도를 예측 분포의 엔트로피(entropy)로 측정한다. 예를 들어, 입력 \(x\)에 대해 출력 \(y\)가 나올 확률 분포가 \(p(y \mid x)\)라고 할 때, 이 분포의 엔트로피는 다음과 같이 정의된다.

\[H(Y \mid x) = - \int p(y \mid x) \log p(y \mid x) \, dy\]

이 값이 높을수록 모델은 불확실하며, 낮을수록 확신을 가지고 있는 것으로 해석된다. 자연어 생성의 경우, 하나의 출력 문장 \(s = (s_1, s_2, \dots, s_n)\) 는 토큰 단위의 조건부 확률로 계산된다. 즉, 문장 전체의 확률은 다음과 같다.

\[p(s \mid x) = \prod_{i=1}^{n} p(s_i \mid s_{<i}, x)\]

따라서 로그 확률은 다음과 같이 계산되며,

\[\log p(s \mid x) = \sum_{i=1}^{n} \log p(s_i \mid s_{<i}, x)\]

이를 통해 전체 문장의 확률 또는 로그 확률을 기반으로 불확실성을 추정한다. 다만, 문장이 길어질수록 곱셈된 확률이 작아지는 문제가 있어, 이를 보완하기 위해 문장 길이로 정규화한 로그 확률도 자주 사용된다.

\[\frac{1}{n} \sum_{i=1}^{n} \log p(s_i \mid s_{<i}, x)\]

이러한 방식은 단어 수가 많은 문장에 불리하게 작용하는 것을 막고, 문장 간의 확률 비교를 보다 공정하게 만든다. 하지만 이런 방식들은 모두 문장 단위의 토큰 시퀀스를 별개로 간주한다는 점에서 한계가 있다. 의미적으로 동일한 문장이라 하더라도 표현이 다르면 서로 다른 확률 항목으로 처리되어, 실제보다 더 높은 불확실성이 계산된다. 자연어에서 같은 의미를 가진 다양한 표현이 가능하다는 점을 고려하면, 이는 근본적인 한계이며 불확실성 측정을 왜곡시킬 수 있다.

더불어 자연어 생성의 출력 공간은 \(O(|T|^N)\) 에 달할 정도로 고차원적이기 때문에, 전체 엔트로피를 계산하기 위해 몬테카를로 샘플링에 의존할 수밖에 없다. 그러나 이 경우 확률이 낮은 문장들(low-probability sequences)이 로그 값에 의해 엔트로피에 과도하게 기여하게 되며, 샘플 수가 부족할 경우 엔트로피 추정이 불안정해진다는 문제가 있다. 더불어 자연어 응답은 길이가 제각각이기 때문에, 길이에 따른 로그 확률의 감소로 인해 긴 문장이 무조건 더 불확실하다고 평가되는 길이 편향(length bias) 문제도 존재한다. 이를 막기 위해 길이 정규화된 엔트로피가 제안되긴 했지만, 항상 이상적인 해법은 아니다. 정답이 짧은 경우(예: TriviaQA)에는 유효할 수 있지만, 다양한 길이의 정답이 존재하는 경우(CoQA 등)에는 오히려 왜곡을 초래할 수 있다.

이처럼 기존의 불확실성 측정 방식은 표현의 다양성과 문장의 구조적 특성을 충분히 반영하지 못하며, 특히 같은 의미를 가진 다양한 표현들에 대해 인위적으로 높은 불확실성을 부여하는 문제가 있다.

의미 기반 불확실성 측정 (Semantic Entropy)

기존의 불확실성 측정 방식은 언어 모델이 생성한 문장을 각기 독립적인 시퀀스로 간주하여 확률을 계산한다. 하지만 자연어에서는 표현이 달라도 의미가 동일한 문장들이 다수 존재한다. 따라서 문장 자체가 아닌, 문장이 담고 있는 의미(semantic meaning)를 기준으로 불확실성을 측정해야 한다는 필요성이 제기되었고, 저자들은 Semantic Entropy라는 새로운 지표를 제안한다. 핵심 아이디어는 다음과 같다. 언어 모델이 생성한 여러 문장 중에서 같은 의미를 가진 문장들을 하나의 ‘의미 집합(semantic class)’으로 묶고, 이 의미 단위로 불확실성을 계산한다는 것이다.

구체적으로, 다음과 같은 3단계 절차를 따른다.

1. 샘플링: 주어진 질문이나 문맥 \(𝑥\) 에 대해 언어 모델로부터 \(𝑀\) 개의 문장 \(s^{(1)},\ s^{(2)},\ \dots,\ s^{(M)}\)을 샘플링한다.
2. 의미 클러스터링: 이들 문장을 서로 의미가 같은 것들끼리 묶는다. 두 문장이 서로를 양방향으로 함의(entailment)하면 같은 의미를 가진 것으로 판단한다.
3. 의미 기반 엔트로피 계산: 같은 의미 집합 내의 문장 확률들을 합산하여 의미 단위의 확률 분포를 만들고, 이에 대한 엔트로피를 계산한다.

이 과정을 수식으로 정리하면 다음과 같다. 먼저 의미 집합 \(𝑐 ∈ 𝐶\) 의 확률은 다음과 같이 정의된다.

\[p(c \mid x) = \sum_{s \in c} p(s \mid x)\]

이제 전체 의미 공간 \(C\)에 대해 Semantic Entropy는 다음과 같이 계산된다.

\[H_{\text{semantic}}(x) = - \sum_{c \in C} p(c \mid x) \log p(c \mid x)\]

이때 실제 모델이 생성하는 문장들은 전체 의미 공간의 일부만 반영하기 때문에, 위 수식은 샘플링 기반 Monte Carlo 근사로 다음과 같이 표현된다:

\[H_{\text{semantic}}(x) \approx - \frac{1}{|C|} \sum_{i=1}^{|C|} \log p(C_i \mid x)\]

이 방식은 표현의 다양성을 허용하면서도 의미의 불확실성만을 측정할 수 있다는 점에서, 기존 방식보다 훨씬 더 직관적이고 신뢰할 수 있는 지표를 제공한다.

🎯 예시: 의미 기반 엔트로피 계산

Semantic Entropy가 기존 방식과 어떻게 다른지를 직관적으로 보여주기 위해, 간단한 예시를 통해 비교해보자. 예를 들어, “프랑스의 수도는 어디인가요?”라는 질문에 대해 언어 모델이 다음과 같은 세 문장을 생성했다고 가정하자.

문장	확률 ( p(s \(\mid\) x) )
A: “파리입니다.”	0.5
B: “프랑스의 수도는 파리예요.”	0.4
C: “런던입니다.”	0.1

기존의 엔트로피 계산 방식은 이 세 문장을 모두 독립적으로 처리하여 다음과 같은 엔트로피를 계산한다.

\[H = - (0.5 * log 0.5 + 0.4 * log 0.4 + 0.1 * log 0.1) ≈ 0.94\]

이 값은 모델이 상당한 불확실성을 갖는 것으로 해석된다. 그러나 A와 B는 의미적으로 동일한 문장이며, 이는 사람이라면 쉽게 인지할 수 있다. 이를 고려해 A와 B를 하나의 의미 집합(semantic class)으로 묶으면, 의미 기반 확률은 다음과 같이 구성된다.

의미 집합 1 (“파리” 관련 답변들):

• 의미 집합 1 (“파리” 관련): 0.5 + 0.4 = 0.9
• 의미 집합 2 (“런던”): 0.1

이제 의미 단위로 엔트로피를 계산하면:

\[H_semantic = - (0.9 * log 0.9 + 0.1 * log 0.1) ≈ 0.33\]

→ 의미를 기준으로 묶으면 실제 불확실성이 훨씬 낮게 측정됨.

즉, 표면적으로는 다양한 답변이 존재하는 것처럼 보였지만, 의미적 기준으로 보면 대부분의 확률이 하나의 정답에 몰려 있으며, 실제 불확실성은 훨씬 낮다는 것을 알 수 있다.

📘 관련 연구

논문은 기존 언어 모델의 불확실성 추정 연구와 차별화된 접근을 시도한다. 대부분의 기존 연구들은 분류(classification) 또는 회귀(regression) 문제에서 예측의 신뢰도를 추정하는 데 집중해왔으며, 이때 사용되는 주요 방법은 확률 보정(calibration)에 초점을 둔다. 대표적인 예로는 Brier score, Monte Carlo Dropout, Deep Ensembles 등이 있으며, 이들은 모델의 예측 확률이 얼마나 실제 정답 확률과 일치하는지를 측정한다.

자연어 생성(NLG)에서의 불확실성 추정에는 다음과 같은 기존 접근 방식들이 있다. 먼저, 예측 엔트로피(Predictive Entropy)는 생성된 문장 자체의 확률 분포로부터 엔트로피를 계산해 불확실성을 추정한다. 이 방식은 일반적으로 확률이 분산되어 있을수록 높은 값을 갖는다. 그러나 이 방식은 긴 문장이 불리하다는 문제를 내포하고 있어, 이를 보정한 방식으로 길이 정규화된 엔트로피(Normalised Entropy)가 사용된다. 이 방법은 전체 로그 확률을 문장 길이로 나누어 엔트로피 값을 보정하는 방식이다. 또한 p(True)는 모델이 정답을 직접 생성할 확률을 기반으로 한 단순한 지표로, “모델이 얼마나 정답에 자신 있는가”를 수치로 나타낸다. 그러나 이 방식은 해당 정답이 단 하나로 정의되어 있어야 하며, NLG처럼 다양한 정답이 존재하는 경우에는 적절하지 않다. Lexical similarity 기반 접근은 Rouge-L 등의 단어 수준 유사도를 통해 예측 품질을 간접 추정한다. 이는 특히 요약(summarization)이나 QA 같은 태스크에서 널리 사용되지만, 표현만 다르고 의미는 같은 문장에 대해 잘못된 불확실성을 추정할 수 있다.

위의 방식들은 대부분 토큰 단위의 시퀀스를 독립적으로 처리하거나, 단일 정답 기준의 확률에 의존한다는 한계가 있다. 표현이 다르지만 의미가 같은 문장들을 각각 독립적으로 취급하면, 실제보다 더 높은 엔트로피가 계산되어 모델이 마치 확신이 없는 것처럼 보이게 된다. 특히 자연어 생성은 표현의 다양성이 중요한 영역이기 때문에, 이러한 방식은 본질적으로 NLG에서의 불확실성 추정에 적합하지 않다. 이러한 한계를 극복하기 위해, 논문은 의미적 동치성을 기반으로 하는 Semantic Entropy를 제안하게 되었으며, 앞서 설명하였듯이 unsupervised 방식으로 작동하며, 의미적으로 동일한 문장들을 하나의 클래스(semantic equivalence class)로 묶어 엔트로피를 계산함으로써, 기존 방식들이 놓치고 있던 “의미 차원의 불확실성”을 정밀하게 측정할 수 있게 한다.

다음 그림은 이러한 다양한 기존 불확실성 추정 방법들과 Semantic Entropy를 비교한 결과를 시각적으로 보여준다. Figure 1.(a)는 30B 파라미터 OPT 모델을 사용해 TriviaQA 데이터셋에 대해 각 방법의 AUROC를 측정한 결과로, Semantic Entropy가 다른 방법들보다 높은 신뢰도 예측 성능을 보임을 보여준다. Figure 1.(b)는 모델 크기에 따른 AUROC 변화를 비교한 것으로, Semantic Entropy가 모델 크기 증가에 따라 가장 일관되게 성능이 향상되며, 작은 모델에서도 다른 방법들보다 안정적인 성능을 유지함을 확인할 수 있다.

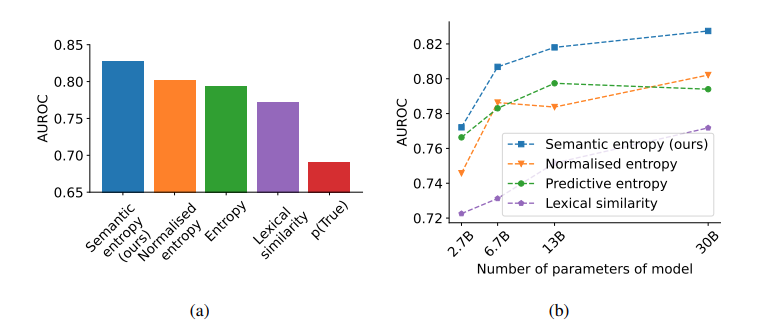
Figure 1: (a) Semantic Entropy의 AUROC 우수성 (b) 모델 크기에 따른 AUROC 비교

📗 실험 및 결과

이 논문은 제안한 Semantic Entropy가 기존의 불확실성 추정 방법들보다 정답과 오답을 더 정확하게 구별할 수 있는지를 실험을 통해 검증한다. 구체적으로, 언어 모델이 자신 있게 한 응답이 실제로 정답일 가능성이 높은지, 또는 불확실해 하는 응답이 실제로 오답인지 여부를 얼마나 잘 판별할 수 있는지를 평가했다.실험에 사용된 모델은 Meta의 OPT(Open Pre-trained Transformer) 시리즈로, 4가지 크기(2.7B, 6.7B, 13B, 30B)의 파라미터를 가진 모델들이 포함되었다. 이는 불확실성 추정 지표가 모델의 크기에 따라 어떻게 성능이 변화하는지를 함께 보기 위한 설정이다.

데이터셋은 두 가지가 사용되었다.

• TriviaQA: 정답을 외워야 하는 유형의 질의응답 태스크로, 문서 없이 바로 답을 생성해야 하는 closed-book QA이다.
• CoQA: 문서를 참고할 수 있는 open-book QA로, 모델이 문맥을 기반으로 답을 생성한다.

정답 여부는 단순한 정확도만으로 판단하지 않고, Rouge-L 점수를 기준으로 했다. Rouge-L은 생성된 문장과 정답 문장 간의 긴 공통 서열(Longest Common Subsequence)을 기반으로 측정되며, 여기서는 0.3 이상이면 정답으로 간주한다. 이 기준은 의미는 같지만 표현이 다른 문장들을 포용할 수 있도록 설계된 것이다. 불확실성 추정 성능을 평가하기 위해 사용된 핵심 지표는 AUROC (Area Under the Receiver Operating Characteristic curve)이다. AUROC는 모델이 “이 응답이 신뢰할 만한가?”를 판단할 때 정답 응답과 오답 응답을 얼마나 잘 구별하는지를 측정한다. AUROC 값이 1에 가까울수록 구분 능력이 뛰어나고, 0.5에 가까우면 무작위 추정과 다를 바 없는 수준이라는 뜻이다.

아래 Figure 2는 두 데이터셋(CoQA와 TriviaQA)에 대해, 모델 크기가 증가함에 따라 다양한 불확실성 지표들의 AUROC가 어떻게 변화하는지를 보여준다.

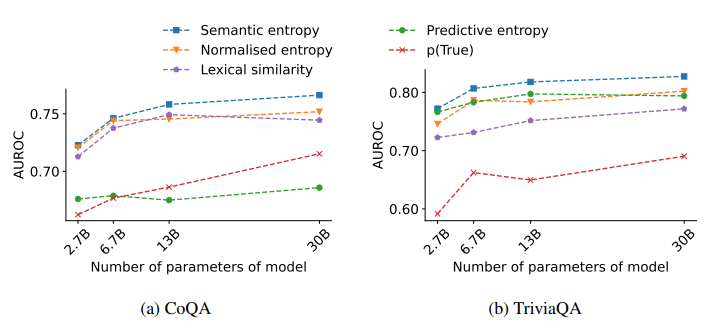
Figure 2: CoQA (a)와 TriviaQA (b)에 대한 다양한 지표의 AUROC 비교.

Figure 2(a)는 CoQA 결과를 나타낸다. 이 경우, 모든 모델 크기에서 Semantic Entropy가 가장 높은 AUROC를 기록했지만, 기존 방법들과의 성능 차이는 비교적 작았다. 즉, CoQA처럼 문서를 참고해도 되는 QA에서는 기존 방식들도 어느 정도 유효하게 작동하지만, 그럼에도 Semantic Entropy가 가장 일관되게 높은 신뢰도 추정 성능을 보였다는 점에서 우수하다. 반면 Figure 2(b)는 TriviaQA 결과로, Semantic Entropy의 성능이 훨씬 두드러지게 나타난다. 특히 p(True)와 Predictive Entropy 같은 기존 지표들은 AUROC가 낮아, 정답과 오답을 명확히 구별하지 못하는 문제를 드러낸다. 반면 Semantic Entropy는 모델 크기가 커질수록 꾸준히 성능이 향상되며, 가장 강력한 신뢰도 추정 지표로 작용했다. 이 실험에서는 Semantic Entropy가 기존 지표들—Predictive Entropy, Normalised Entropy, p(True), Lexical Similarity—보다 consistently 더 높은 AUROC를 기록했다. 즉, 모델이 실제로 혼란스러울 때 의미적으로 다양한 응답을 많이 생성하는 경향을 Semantic Entropy가 정확히 포착한다는 것이다.

이를 더 정량적으로 보자면, 의미적으로 같은 응답을 하나의 클러스터로 묶었을 때 그 의미 집합(semantic cluster)의 수가 정답과 오답 간에 차이가 있었다.

• TriviaQA의 경우 정답일 때 평균 1.89개, 오답일 때 평균 3.89개의 의미 집합이 생성되었다.
• CoQA의 경우 정답은 평균 1.27개, 오답은 평균 1.77개로, 오답일수록 모델이 다양한 의미를 생성하며 더 혼란스러워하는 양상을 보였다.

이는 Semantic Entropy가 단순히 확률 분포가 퍼져 있는 정도만 보는 것이 아니라, 의미 차원에서의 다양성을 통해 모델의 불확실성을 정확히 추정할 수 있다는 것을 보여준다.

샘플링 하이퍼파라미터 분석

Figure 3: 샘플 수 및 샘플링 temperature가 Semantic Entropy 성능에 미치는 영향. (a) AUROC vs. 샘플 수, (b) AUROC 및 정확도/다양성 vs. temperature

Semantic Entropy는 샘플링 기반으로 동작하기 때문에, 몇 개의 응답을 샘플링하느냐, 어떤 temperature 설정으로 샘플링하느냐에 따라 성능이 달라질 수 있다. Figure 3은 두 가지 요소—샘플 수와 temperature—가 Semantic Entropy의 AUROC 및 출력 다양성에 미치는 영향을 정량적으로 분석한 결과를 보여준다.

왼쪽의 두 그래프는 각각 CoQA (top)와 TriviaQA (bottom)에서 샘플 수가 증가함에 따라 AUROC가 어떻게 변하는지를 보여준다. 전반적으로 Semantic Entropy는 단 3~5개의 샘플만으로도 기존 방식보다 더 높은 성능을 보이며, 샘플 수가 10개까지 늘어나도 안정적으로 AUROC가 증가한다. 반면, 기존의 Predictive Entropy나 Length-normalized Entropy는 증가 폭이 작거나 거의 일정하다. 이 결과는 Semantic Entropy가 샘플 효율(sample efficiency)이 뛰어나다는 점을 시사한다.

오른쪽의 두 그래프는 샘플링 temperature를 조절했을 때 Semantic Entropy가 어떻게 달라지는지를 보여준다. 위 그래프에서는 temperature가 0.5일 때 AUROC가 가장 높게 나타났으며, 이는 정확도와 다양성 사이의 균형이 가장 잘 맞는 지점이라는 것을 의미한다. 아래 그래프에서는 temperature가 높아질수록 생성되는 문장의 다양성은 증가하지만, 평균 정확도는 감소하는 경향을 보인다.

따라서 Semantic Entropy를 실질적으로 사용할 때는 적절한 temperature 설정과 소수의 고품질 샘플만으로도 높은 신뢰도 예측 성능을 얻을 수 있다는 실용적인 시사점을 제공한다.