On Calibration of Modern Neural Networks

📄 논문 정보

“On Calibration of Modern Neural Networks” (ICML 2017)

📌 연구 개요

Confidence Calibration은 모델이 예측한 확률이 실제 정답일 가능성과 얼마나 일치하는지를 나타내는 개념이다. 예를 들어, 어떤 이미지에 대해 모델이 고양이일 확률을 0.9라고 예측했을 때, 이러한 예측이 잘 보정(calibrated)되어 있다면 실제로 그 이미지가 고양이일 확률도 약 90%가 되어야 한다는 것이다.

On Calibration of Modern Neural Networks 논문은 빠르게 발전하고 연구되어져 오고 있는 ResNet, DenseNet 등과 같은 현대적인 신경망 모델들이 높은 분류 정확도를 달성함에도 불구하고, 오히려 확률 보정(calibration) 성능은 더 나빠졌다는 사실을 실험적으로 보이고 있다. 과거의 얕은 신경망 모델들은 예측 확률이 실제 정답 확률과 비교적 잘 일치했지만, 깊고 복잡한 구조를 가진 최신 모델들은 자신 있게 예측을 하면서도 그 확률이 실제 정답률과 불일치하는 경향이 있다는 점을 짚고 있다. 한 마디로 말해 최신 모델들은 Overconfident 되어져 있다는 점을 발견하였다.

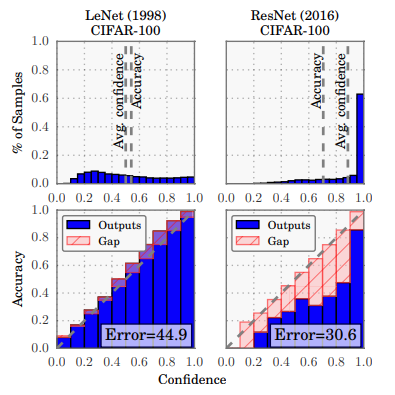Figure 1: Confidence histograms (top) and reliability diagrams (bottom) for a 5-layer LeNet (left) and a 110-layer ResNet (right) on CIFAR-100. Refer to the text below for detailed illustration.

이러한 문제는 자율주행, 의료 진단, 법률 판단 등과 같이 예측 결과에 대한 신뢰도가 매우 중요한 응용 분야에서 특히 도드라질 수 있기에 모델이 단순히 정확할 뿐만 아니라, 자신의 예측이 얼마나 확실한지에 대한 표현 또한 신뢰할 수 있어야 한다.

본 논문에서는 이러한 문제를 해결하기 위해 다양한 사후 보정(post-hoc calibration) 방법들을 실험적으로 비교하고, 그 중에서도 Temperature Scaling이라는 단 하나의 스칼라 파라미터만을 사용하는 간단한 방법이 매우 효과적이라는 사실을 밝혀냈다. 본 글에서는 이의 실험 코드도 구현하였다.

---

🔍 신경망의 Overconfidence 원인 분석

최근의 신경망 모델들은 높은 정확도를 자랑하지만, 그 confidence (예측 확률) 는 실제 정답률과 잘 맞지 않는 경우가 많다. 이 현상을 miscalibration (불완전한 보정) 이라고 하며, 그 원인과 관련 요소들을 우선 분석하였다.

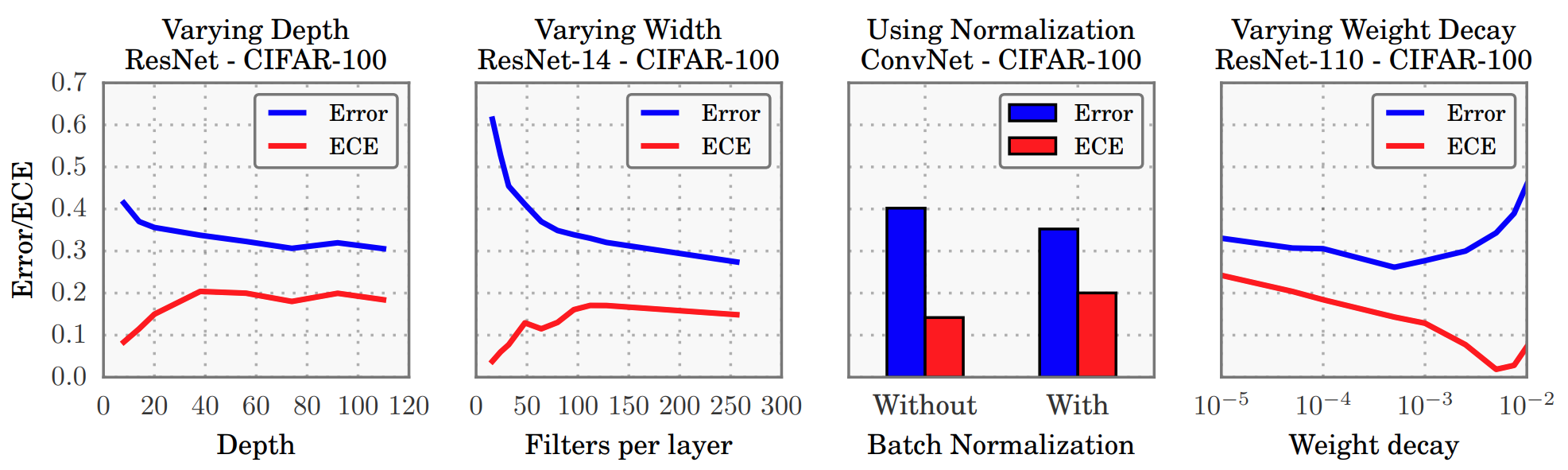Figure 2: The effect of network depth (far left), width (middle left), Batch Normalization (middle right), and weight decay (far right) on miscalibration, as measured by ECE (lower is better)

1. 모델 용량의 증가 (Model Capacity)

• 최근 딥러닝 모델들은 레이어 수와 필터 수가 급격히 증가하여, 학습 데이터를 더 잘 맞출 수 있는 모델 용량(capacity) 을 갖추게 되었다.
• 하지만 모델 용량이 커질수록 오히려 confidence가 실제 정확도보다 과도하게 높아지는 과신, 즉 overconfidence 하는 경향이 나타난다.

실험 결과 (ResNet on CIFAR-100):

• 깊이(depth)를 증가시키면 Error은 줄어드나 ECE가 증가
• 필터 수(width)를 증가시키면 Error은 확연히 줄어드나, ECE가 증가

높은 capacity는 overfitting을 야기할 수 있으며, 이러한 경우 정확도는 좋아져도 확률의 품질은 나빠진다.

---

2. Batch Normalization의 영향

• Batch Normalization은 딥러닝 모델의 학습을 안정화시키고 빠르게 만드는 기법으로, 현대 아키텍처에서 필수적으로 사용된다.
• 하지만, BN을 사용한 모델들은 정확도는 올라가지만 calibration은 오히려 나빠지는 현상이 나타난다.

실험 결과 (6-layer ConvNet on CIFAR-100):

• BN을 적용한 ConvNet은 정확도가 약간 올라가지만(Error 감소), ECE는 뚜렷하게 증가

BN은 내부 활성 분포를 정규화하여 학습을 더 잘 되게 하지만, 결과적으로 출력 확률이 더 과신된(overconfident) 상태로 나타나 calibration에는 부정적인 영향을 미치게 된다.

---

3. Weight Decay 감소의 영향

• 전통적으로 weight decay 는 과적합을 막기 위한 정규화 방법으로 널리 사용되어 왔으며, overfitting을 방지하기 위해 가중치에 패널티를 주는 정규화 기법이다.
• 최근에는 BN의 정규화 효과 때문에 weight decay 사용량이 줄어드는 추세이다.
• 하지만 실험에서는 weight decay를 증가시킬수록 calibration은 개선되는 경향을 보인다.

실험 결과 (ResNet-110 on CIFAR-100):

• Weight decay를 증가시키면 분류 정확도(Error)는 특정 구간에서 최적점을 찍고 이후 다시 증가
• ECE는 weight decay가 증가할수록 감소하는 경향을 보임

즉, 정확도를 최대화하는 weight decay 설정과 calibration을 최적화하는 설정은 서로 다를 수 있으며, 정확도는 유지되더라도 confidence는 왜곡될 수 있다.

---

4. NLL 과적합 현상 (Overfitting to NLL)

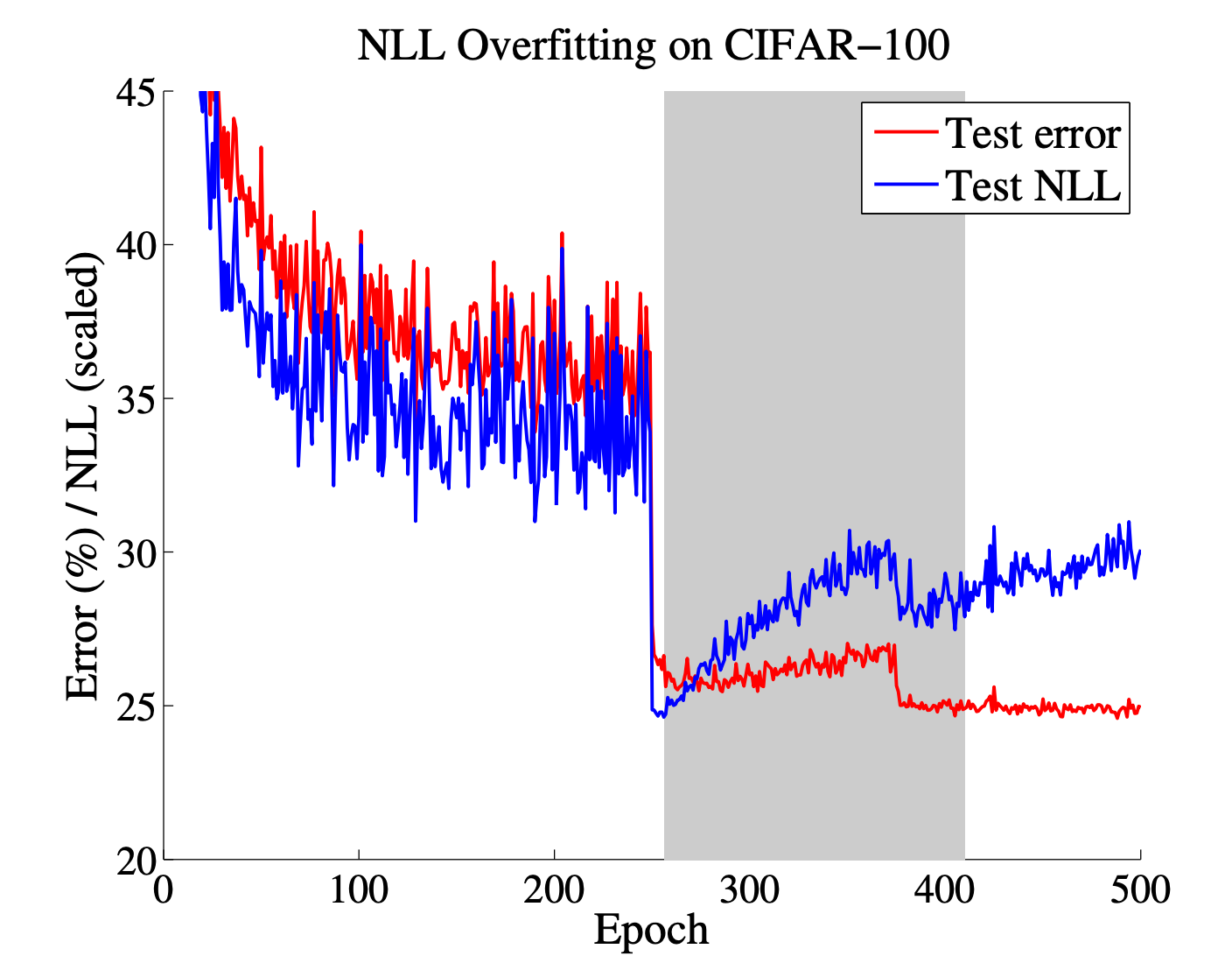Figure 3: Test error and NLL of a 110-layer ResNet with stochastic depth on CIFAR-100 during training

• 실험에서는 learning rate가 낮아지는 구간에서 test error는 계속 줄어드는 반면, NLL은 다시 증가하는 현상을 확인하였다.
• 이는 모델이 정확도는 높이지만 confidence가 실제보다 과도한 상태로 학습이 진행되고 있음을 의미한다.

실험 결과 (ResNet-110 + stochastic depth on CIFAR-100):

• Epoch 250 이후 learning rate 감소
• 이후 test error는 감소 (29% → 27%)하지만, NLL은 증가

최신 신경망은 학습 후반부에서 NLL을 계속 최소화하려는 과정에서 confidence를 과도하게 높이는 경향이 있으며, 이로 인해 실제 정답률보다 높은 확률을 출력하는 overconfident한 상태로 calibration 오류가 발생한다.

---

📐 Calibration의 정의 및 측정 방법

본 논문에서는 다중 클래스 분류 문제를 다루고 있으며, 딥러닝 모델은 주어진 입력 \(X \in \mathcal{X}, \quad Y \in \{1, \dots, K\}\) 를 예측하는다고 가정한다. 모델의 예측 확률은 다음과 같이 정의된다.

\[h(X) = (\hat{Y}, \hat{P})\]

여기서 \(\hat{Y}\)는 예측된 클래스, \(\hat{P}\)는 각 클래스에 대한 확률 분포이며, softmax 출력의 최댓값으로 정의된다.

그럼 완벽하게 보정된 모델의 정의는 어떻게 될까? 본 논문에서는 다음과 같이 정의하고 있다.

\[P(\hat{Y} = Y \mid \hat{P} = p) = p, \quad \forall p \in [0, 1]\]

위 식에서 알 수 있듯이 모델이 완벽히 보정(calibrated)되어 있다는 것은, 예측한 확률 값이 실제 정답률과 일치하는 것을 의미한다. 예를 들어 모델이 100개의 샘플에 대해 모두 0.8의 confidence를 출력했다면, 실제로 그 중 약 80개가 맞아야 완벽히 보정된 것이다.

🔍 Reliability Diagram (신뢰도 다이어그램)

예측 확률 \(\hat{P}\)를 구간으로 잘게 나누고, 각 구간에서의 실제 정답률(accuracy)과 평균 confidence를 비교한다. 만약 모델이 잘 보정되어져 있다면, 각 구간에서는 아래의 관계식이 성립해야한다는 것이다.

\[\text{acc}(B_m) = \frac{1}{|B_m|} \sum_{i \in B_m} \mathbf{1}(\hat{y}_i = y_i)\] \[\text{conf}(B_m) = \frac{1}{|B_m|} \sum_{i \in B_m} \hat{p}_i\] \[\text{Accuracy}(B_m) \approx \text{Confidence}(B_m)\]

여기서 \(\text{acc}(B_m)\)는 구간 \(B_m\)에 속하는 샘플들의 실제 정답률, \(\text{conf}(B_m)\)는 구간 \(B_m\)에 속하는 샘플들의 평균 confidence를 의미한다. 만약 모델이 잘 보정되어 있다면, 두 값은 서로 비슷해야 한다.

📏 Expected Calibration Error (ECE)

ECE는 모델의 전체 calibration 성능을 수치적으로 측정하는 대표적인 지표로, 각 bin에 대해 예측 확률과 실제 정답률 간의 차이를 평균하여 계산한다. \(M\)개의 bin으로 나누고, 각 bin \(B_m\)에 대해 다음과 같이 정의된다.

\[\text{ECE} = \sum_{m=1}^{M} \frac{|B_m|}{n} \left| \text{acc}(B_m) - \text{conf}(B_m) \right|\]

📏 Maximum Calibration Error (MCE)

MCE는 가장 큰 오차를 보인 bin의 calibration gap을 측정하게 되며, 쉽게 말해 “최악의 보정 실패” 정도를 나타낸다고 생각할 수 있다. 안전이 중요한 시스템에서 매우 중요한 지표로 사용될 수 있다.

\[\text{MCE} = \max_{m \in \{1, \dots, M\}} \left| \text{acc}(B_m) - \text{conf}(B_m) \right|\]

---

🛠️ Calibration Methods

본 논문에서는 이미 학습된 모델에 대해 확률 보정을 위한 사후 처리(Post-hoc) 방법들을 소개하고 있으며, 이들은 모델의 예측 구조나 정확도는 유지하면서, 예측 확률(confidence)이 실제 정답률과 더 잘 일치하도록 만들어준다.

📘 1. Calibrating Binary Models

우선 다룰 내용은 이진 분류(binary classification) 상황에서의 confidence calibration 기법들을 알아보고자 한다. 이 경우 클래스 라벨은 \(Y \in \{0, 1\}\)이며, 모델은 positive 클래스(1)에 대한 확률 \(\hat{p}_i\)와 logit \(z_i \in \mathbb{R}\)를 출력한다. 확률은 보통 sigmoid 함수를 통해 다음과 같이 계산된다:

\[\hat{p}_i = \sigma(z_i) = \frac{1}{1 + \exp(-z_i)}\]

Calibration은 \(\hat{p}_i\) 또는 \(z_i\)를 조정하여 새로운 calibrated 확률 \(\hat{q}_i\)를 얻는 것이다.

A. Histogram Binning

Histogram Binning은 모델이 출력하는 확률을 일정 구간(bin)으로 나누고, 각 구간 내에서의 실제 정답 비율을 새로운 보정 확률로 사용하는 방법이다. 모든 \(\hat{p}_i\)를 \(M\)개의 구간 \(B_1, B_2, ..., B_M\)으로 나눈다. 각 bin마다 정답률을 계산하여 그 값을 보정된 확률로 사용한다. 이를 수식으로 살펴보면 다음과 같다.

• 구간 정의: \(B_m = (a_m, a_{m+1}]\) where \(0 = a_1 \leq a_2 \leq \dots \leq a_{M+1} = 1\)
• 최적화 문제: \(\min_{\theta_1,\dots,\theta_M} \sum_{m=1}^{M} \sum_{i=1}^{n} \mathbf{1}(a_m \leq \hat{p}_i < a_{m+1}) (\theta_m - y_i)^2\)

위의 최적화 문제를 풀게되면 각 bin의 보정 확률은 bin 내 레이블 평균으로 계산되게 된다.

\[\theta_m = \frac{1}{|B_m|} \sum_{i \in B_m} y_i\]

예시를 통해 살펴보도록 Histogram Binning을 살펴보도록 하겠다.

• 예측 확률과 실제 정답

샘플 번호	예측 확률 \(\hat{p}\_i\)	실제 정답 \(y\_i\)
1	0.15	0
2	0.22	1
3	0.35	1
4	0.48	0
5	0.63	1
6	0.72	1
7	0.85	1
8	0.89	0
9	0.95	1

• 예측 확률을 bin으로 나눈 결과

Bin 번호	확률 구간	해당 샘플 번호	정답 목록	보정 확률 \(\theta\_m\)
1	(0.0, 0.3]	1, 2	[0, 1]	0.50
2	(0.3, 0.7]	3, 4, 5	[1, 0, 1]	0.67
3	(0.7, 1.0]	6, 7, 8, 9	[1, 1, 0, 1]	0.75

• 각 bin에서의 실제 정답 평균 (보정 확률)

Bin 번호	정답 목록	보정 확률 \(\theta\_m\)
1	[0, 1]	0.50
2	[1, 0, 1]	0.67
3	[1, 1, 0, 1]	0.75

구현이 간단하고 어떤 모델이든 사후 보정으로 적용할 수 있으나, 예측이 계단 함수처럼 변경되어 부드럽지 않으며 bin을 몇 개 가지느냐에 따라 성능이 크게 변화할 수 있다.

B. Isotonic Regression

$\hat{p}_i$에 대해 단조 증가(monotonic) 함수 $f$를 학습하여:

\[\hat{q}_i = f(\hat{p}_i)\]

• 목적 함수: \(\min_f \sum_{i=1}^n (f(\hat{p}_i) - y_i)^2 \quad \text{subject to } f \text{ is monotonic}\)

이 방법은 histogram보다 유연하지만, 과적합의 가능성이 있으며 정규화가 필요할 수 있다

C. Platt Scaling

모델이 출력한 logit $z_i$를 입력으로 사용하여, sigmoid를 적용한 로지스틱 회귀를 수행함:

\[\hat{q}_i = \sigma(az_i + b) = \frac{1}{1 + \exp(-(az_i + b))}\]

• $a$, $b$는 validation set에서 NLL을 최소화하도록 학습
• 신경망 파라미터는 고정됨

정확도는 그대로 유지하면서 확률을 조정할 수 있는 간단한 방법.

D. BBQ (Bayesian Binning into Quantiles)

Histogram Binning의 확장으로, 여러 binning scheme을 고려하여 Bayesian model averaging을 수행한다.

• calibrated 확률: \(P(\hat{q}_i | \hat{p}_i, D) = \sum_{s \in \mathcal{S}} P(\hat{q}_i | s, \hat{p}_i, D) \cdot P(s | D)\)

• 여기서 $s$는 binning scheme이며, prior는 Beta 분포, likelihood는 binomial로 계산됨

정확하지만 구현이 복잡하고 계산량이 많음.

📘 2. Extension to Multiclass Models

물론입니다. 아래는 📘 2. Extension to Multiclass Models 내용을 수식 포함 마크다운 형식으로 한 번에 복사할 수 있도록 정리한 것입니다:

---

📘 2. Extension to Multiclass Models

다중 클래스 분류 문제에서는 각 입력 샘플 \(x_i\)에 대해 logit 벡터 \(z\)를 softmax에 입력하여 다음과 같이 확률을 계산한다.

\[\hat{P} = \max_k \left( \frac{e^{z_k}}{\sum_j e^{z_j}} \right)\]

A. Matrix Scaling

Logit 벡터 \(z\)에 대해 선형 변환 \(Wz + b\)를 적용하고 softmax를 취한다.

\[\hat{q} = \text{softmax}(Wz + b)\]

• \(W \in \mathbb{R}^{K \times K}\), \(b \in \mathbb{R}^K\)
• 매우 유연한 표현이 가능하지만, 파라미터 수가 많아 과적합 가능성이 존재한다.

B. Vector Scaling

Matrix Scaling을 간소화한 버전으로, \(W\)를 대각 행렬 \(D\)로 제한한 것이다.

\[\hat{q} = \text{softmax}(Dz + b)\]

• 파라미터 수는 \(2K\)개로 줄어들며, 계산 효율성과 과적합 가능성이 줄어든다.

C. Temperature Scaling

가장 간단하면서도 강력한 보정 기법으로 logit을 \(T\)로 나누고 softmax 적용한다.

\[\hat{q} = \text{softmax}(z / T)\]

• ( T > 1 ): 확률이 분산됨
• ( T = 1 ): 원래 모델과 동일
• ( T < 1 ): 확률이 더 sharp해짐

---

🎯 실험 목적

현대 딥러닝 모델은 높은 분류 정확도를 달성하지만, 예측 확률은 과신(overconfidence)되는 경향이 있는 것을 앞서 살펴보았으며, 다양한 사후 확률 보정(post-hoc calibration) 기법들을 정리하였다. 이들을 비교하고 가장 효과적인 방법을 식별하고자 한다.

• 모델: ResNet, Wide ResNet, DenseNet, LeNet, DAN, TreeLSTM
• 데이터셋: CIFAR-10, CIFAR-100, ImageNet, SVHN, Birds, Cars, 20News, Reuters, SST
• 평가지표: Expected Calibration Error (ECE), Maximum Calibration Error (MCE), Negative Log Likelihood (NLL), Error Rate

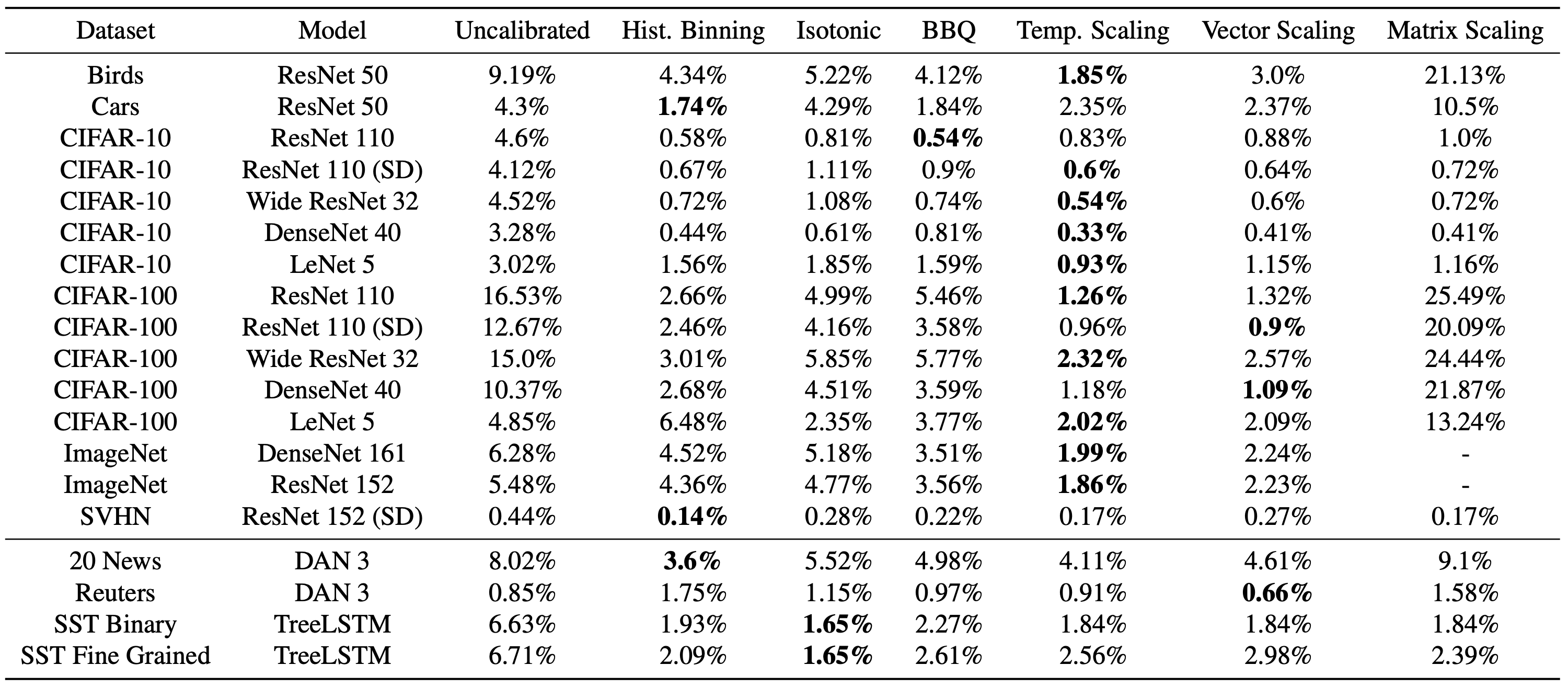Figure 5: ECE (%) (with M = 15 bins) on standard vision and NLP datasets before calibration and with various calibration methods. The number following a model’s name denotes the network depth.

논문은 현대 신경망들이 높은 정확도에도 불구하고 예측 확률이 과도하게 자신감(overconfident)을 가진다는 문제를 지적하고 있으며, Temperature Scaling은 단 하나의 파라미터만으로 대부분의 경우 가장 우수한 보정 성능(ECE 감소)을 보여주었다. 다른 복잡한 보정 기법들보다 간단하고 안정적으로 작동하며, 정확도를 떨어뜨리지 않고 확률만 조정할 수 있다는 것을 확인할 수 있었으며, CIFAR-100 등 다양한 데이터셋에서 ECE가 최대 16% → 1% 수준으로 크게 감소하였다.

🧪 Python 실습 개요

지금부터는 앞서 살펴본 논문과 관련하여 실습을 진행해보고자 한다. 본 실험은 CIFAR-100 이미지 분류 과제를 대상으로 ResNet-34 모델의 신뢰도 보정(calibration) 성능을 정량적으로 평가하고 시각화하는 것을 목적으로 한다. 딥러닝 분류 모델은 일반적으로 높은 분류 정확도를 달성할 수 있으나, 출력 확률이 실제 정답일 가능성을 과대평가하는 과신(overconfidence) 현상을 자주 나타낸다. 이러한 문제는 실제 응용에서 모델의 불확실성을 신뢰할 수 없게 만든다. 앞서 살펴본 논문에서는 이러한 문제를 해결하기 위한 다양한 Post-hoc 보정 기법들을 제안하고 있으며, 이 중 하나인 Temperature Scaling을 직접 구현하고, 그 효과를 Reliability Diagram을 통해 시각적으로 분석해보고자 한다.

모델 학습에는 CIFAR-100 데이터셋과 ResNet-34 모델 구조를 사용하였다. CIFAR-100은 총 100개의 레이블로 구성된 컬러 이미지 데이터셋으로, 각 이미지는 32×32 해상도의 RGB 이미지이다. 각 클래스당 500개의 학습 이미지와 100개의 테스트 이미지가 포함되어 있으며, 총 50,000개의 학습 샘플과 10,000개의 테스트 샘플을 포함한다. 분류 모델로 사용된 ResNet-34는 Residual Network 계열의 대표적인 구조 중 하나로, 34개의 층을 갖는 심층 합성곱 신경망이다. 잔차 연결(residual connection)을 통해 깊은 네트워크에서 발생하는 기울기 소실 문제를 효과적으로 해결할 수 있으며, CIFAR-100과 같은 중간 난이도의 이미지 분류 문제에 널리 사용된다. 본 실험에서는 사전 학습 없이 처음부터 CIFAR-100에 대해 ResNet-34를 학습시켰으며, 출력층 fully-connected layer의 출력 차원을 100으로 설정하여 100개의 클래스를 분류하도록 구성하였다.

본 실험에서는 학습된 ResNet-34 모델을 기준으로 T ∈ \({0.5, 1.0, 1.5, 2.0}\) 범위에 대해 Temperature Scaling을 적용한 후, 다음과 같은 관점에서 보정 성능을 평가하였다:

1. Reliability Diagram을 통해 confidence vs accuracy 관계를 시각화
2. Expected Calibration Error (ECE) 수치를 계산하여 정량적 보정 성능 평가
3. 각 confidence bin 내의 sample 수 및 정확도 변화 분석

그럼 지금부터는 단계별로 코드를 살펴보도록 하겠다.

1. CIFAR-100 데이터셋의 정규화를 위한 평균 및 표준편차 계산

딥러닝 모델을 학습할 때, 입력 이미지 데이터를 정규화(normalization) 하는 것은 매우 중요한 전처리 과정이다. 보통 정규화는 각 채널(R, G, B)에 대해 평균을 빼고 표준편차로 나누는 방식으로 이루어진다. 이 과정을 통해 입력 값의 분포를 0을 중심으로 정규화함으로써, 학습이 더 안정적으로 이루어지고 수렴 속도가 빨라질 수 있다.

from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch

transform = transforms.ToTensor()
trainset = datasets.CIFAR100(root='./data', train=True, download=True, transform=transform)
loader = DataLoader(trainset, batch_size=50000, shuffle=False)

data = next(iter(loader))[0]  # (50000, 3, 32, 32)
mean = data.mean(dim=(0, 2, 3))
std = data.std(dim=(0, 2, 3))

print("CIFAR-100 평균:", mean)
print("CIFAR-100 표준편차:", std)

위 코드를 실행하게 되면 CIFAR-100 데이터셋이 로컬에 저장되어져 있지 않은 경우 ./data 경로에 저장하게 되며 이후 전체 학습 데이터에 대한 평균과 표준편차를 계산하게 된다.

2. CIFAR-100 데이터를 이용한 ResNet-34 학습

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms, models
from torch.utils.data import DataLoader

# ---------------- 하이퍼파라미터 설정 ----------------
batch_size = 128
epochs = 30
lr = 0.1
save_path = "모델 저장 경로"
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# ---------------- 데이터 전처리 및 로딩 ----------------
# cifar100_mean_std.py 출력 결과
mean = (0.5071, 0.4866, 0.4409)
std = (0.2673, 0.2564, 0.2762)

# 학습용 데이터에 대해 데이터 증강 및 정규화 수행
transform_train = transforms.Compose([
    transforms.RandomCrop(32, padding=4),         # 무작위 crop (32x32 유지)
    transforms.RandomHorizontalFlip(),            # 무작위 좌우 반전
    transforms.ToTensor(),                        # 텐서 변환 (0~1)
    transforms.Normalize(mean, std)               # 채널별 정규화
])

# CIFAR-100 학습 데이터셋 로드
trainset = datasets.CIFAR100(root='./data', train=True, download=True, transform=transform_train)
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=8)

# ---------------- 모델 정의 ----------------
model = models.resnet34(weights=None)
model.fc = nn.Linear(model.fc.in_features, 100)
model = model.to(device)

# ---------------- 손실 함수 및 옵티마이저 ----------------
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=5e-4)
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1)  # 10 epoch마다 학습률 감소

# ---------------- 학습 루프 ----------------
for epoch in range(epochs):
    model.train()  # 학습 모드 활성화
    running_loss = 0.0
    correct = 0
    total = 0

    for inputs, labels in trainloader:
        inputs, labels = inputs.to(device), labels.to(device)
        optimizer.zero_grad()              # 기울기 초기화
        outputs = model(inputs)            # 순전파
        loss = criterion(outputs, labels)  # 손실 계산
        loss.backward()                    # 역전파
        optimizer.step()                   # 가중치 업데이트

        running_loss += loss.item()
        _, predicted = outputs.max(1)
        total += labels.size(0)
        correct += predicted.eq(labels).sum().item()

    acc = 100. * correct / total
    print(f"[Epoch {epoch+1}/{epochs}] Loss: {running_loss:.3f}, Train Accuracy: {acc:.2f}%")
    scheduler.step()

# ---------------- 학습된 모델 저장 ----------------
torch.save(model.state_dict(), save_path)
print(f"💾 Model saved to: {save_path}")

위의 코드는 ResNet-34를 CIFAR-100 데이터셋을 이용하여 학습하는 과정을 나태내었다. 1번에서 계산된 평균과 표준편차 값을 transforms.Normalize(mean, std) 함수에 그대로 적용하였다. 이 정규화 과정은 데이터 전처리 파이프라인에 포함되어 있으며, 무작위 자르기(RandomCrop), 좌우 반전(RandomHorizontalFlip), 텐서 변환(ToTensor) 이후 마지막 단계에서 수행된다. 정규화된 데이터는 이후 ResNet-34 모델에 입력되며, 이 모델은 출력층만 CIFAR-100의 100개 클래스에 맞게 수정된 형태로 사용된다.

딥러닝 모델, 특히 깊은 구조의 ResNet-34와 같은 모델은 입력의 분포가 지나치게 편향되어 있을 경우 학습이 잘 되지 않거나, 초기 학습 단계에서 매우 느린 수렴 속도를 보일 수 있다. 따라서 사전에 데이터셋의 통계 정보를 기반으로 정규화를 수행하는 것은 학습 성능을 안정시키는 핵심적인 요소다. 결과적으로, 1번의 정규화 값 계산은 2번의 효과적인 모델 학습을 위한 필수 전처리 과정이며, 전체 학습 파이프라인의 신뢰성과 효율성을 높이는 데 중요한 역할을 한다.

모델 학습은 총 30번의 epoch에 걸쳐 진행되며, 한 번의 epoch마다 전체 CIFAR-100 학습 데이터를 한 번씩 순회하게 된다. 학습 과정에서 손실 함수는 다중 클래스 분류에 적합한 CrossEntropyLoss를 사용하며, 옵티마이저는 확률적 경사 하강법(SGD: Stochastic Gradient Descent)에 momentum과 weight decay를 추가하여 안정적인 최적화를 유도한다. 학습률은 초기에 0.1로 설정되며, StepLR 스케줄러를 통해 10 에폭마다 1/10씩 감소시킨다. 이는 초반에는 빠르게 학습하고, 후반에는 천천히 fine-tuning하도록 유도하는 것이다. 모델은 학습 모드(model.train())에서 각 배치 데이터를 순전파(forward)시켜 예측 결과를 출력하고, 이 결과를 실제 정답과 비교하여 손실(loss)을 계산한 후, 역전파(backward)를 통해 가중치의 기울기를 구하고 이를 바탕으로 파라미터를 업데이트한다. 또한 각 epoch마다 누적된 손실과 정확도를 출력하여 학습이 어떻게 진행되고 있는지 확인할 수 있다. 마지막으로 학습이 종료된 후에는 모델의 학습된 가중치 파라미터를 .pth 파일로 저장하여 학습된 모델을 추후 활용할 수 있도록 한다.

3. Reliability Diagram 시각화

이번에는 앞서 학습이 완료된 ResNet-34 모델을 불러와, CIFAR-100 테스트셋에 대해 예측을 수행한 후, 예측의 신뢰도(confidence)와 실제 정답 여부 간의 관계를 분석하고 시각화한다. 이를 위해 Expected Calibration Error (ECE) 를 수치로 계산하고, Reliability Diagram을 통해 모델의 신뢰도가 얼마나 잘 보정되어 있는지를 시각적으로 평가한다.

import torch
import torch.nn.functional as F
from torchvision import datasets, transforms, models
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import os

# ✅ 디바이스 설정 및 모델 로드
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = models.resnet34(weights=None)
model.fc = torch.nn.Linear(model.fc.in_features, 100)
model.load_state_dict(torch.load("./snapshots/resnet34_cifar100_exp/resnet34_cifar100.pth", map_location=device))
model = model.to(device)

# ✅ CIFAR-100 테스트셋 준비
mean = (0.5071, 0.4866, 0.4409)
std = (0.2673, 0.2564, 0.2762)
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(mean, std)
])
test_dataset = datasets.CIFAR100(root="./data", train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False)

# ✅ ECE 계산 및 Reliability Diagram 생성
def compute_reliability_and_ece(model, dataloader, device, n_bins=15):
    model.eval()
    bin_boundaries = torch.linspace(0, 1, n_bins + 1).to(device)
    bin_corrects = torch.zeros(n_bins).to(device)
    bin_confidences = torch.zeros(n_bins).to(device)
    bin_counts = torch.zeros(n_bins).to(device)
    total_samples = 0

    with torch.no_grad():
        for images, labels in dataloader:
            images, labels = images.to(device), labels.to(device)
            logits = model(images)
            probs = F.softmax(logits, dim=1)
            confs, preds = torch.max(probs, dim=1)
            corrects = preds.eq(labels)

            total_samples += labels.size(0)

            for i in range(n_bins):
                in_bin = (confs > bin_boundaries[i]) & (confs <= bin_boundaries[i+1])
                bin_counts[i] += in_bin.sum()
                if in_bin.sum() > 0:
                    bin_corrects[i] += corrects[in_bin].float().sum()
                    bin_confidences[i] += confs[in_bin].sum()

    nonzero = bin_counts > 0
    accs = bin_corrects[nonzero] / bin_counts[nonzero]
    confs = bin_confidences[nonzero] / bin_counts[nonzero]
    bin_centers = ((bin_boundaries[:-1] + bin_boundaries[1:]) / 2)[nonzero]
    filtered_counts = bin_counts[nonzero]

    ece = torch.sum((filtered_counts / total_samples) * torch.abs(accs - confs)).item()
    return bin_centers.cpu(), accs.cpu(), confs.cpu(), ece

def draw_reliability_diagram(bin_centers, accs, confs, ece, name, save_dir):
    os.makedirs(save_dir, exist_ok=True)
    width = 1.0 / len(bin_centers)

    plt.figure(figsize=(5, 5))
    plt.bar(bin_centers, accs, width=width * 0.9, color='blue', edgecolor='black', alpha=0.8, label="Accuracy")
    plt.plot([0, 1], [0, 1], linestyle='--', color='gray', label="Perfect Calibration")
    for x, acc, conf in zip(bin_centers, accs, confs):
        lower = min(acc, conf)
        upper = max(acc, conf)
        plt.fill_between([x - width / 2, x + width / 2], lower, upper,
                         color='red', alpha=0.3, hatch='//')

    plt.xlabel("Confidence")
    plt.ylabel("Accuracy")
    plt.title(f"Reliability Diagram: {name}")
    plt.text(0.02, 0.6, f"ECE = {ece * 100:.2f}%", fontsize=12,
             bbox=dict(facecolor='lavender', edgecolor='gray'))
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.savefig(os.path.join(save_dir, f"{name}_reliability.png"))
    plt.close()

# ✅ 실행
bin_centers, accs, confs, ece = compute_reliability_and_ece(model, test_loader, device)
draw_reliability_diagram(bin_centers, accs, confs, ece, name="ResNet34_CIFAR100", save_dir="./snapshots/resnet34_cifar100_exp")

위 코드는 학습된 모델을 CIFAR-100 테스트 데이터에 적용하여 예측을 수행한 후, 예측 결과에 대한 confidence score와 실제 정답 여부를 비교하여 신뢰도(calibration)를 평가하는 과정을 수행한다. compute_reliability_and_ece 함수는 confidence 값 범위를 일정한 간격으로 나눈 bin을 기준으로 각 bin 내의 평균 confidence와 실제 정확도(accuracy)를 계산하며, 이를 바탕으로 Expected Calibration Error (ECE)를 수치로 반환한다. 이 값이 작을수록 모델의 예측 확률이 실제 정답률과 잘 일치한다는 것을 의미한다.

또한, draw_reliability_diagram 함수는 이러한 정보를 바탕으로 신뢰도 그래프를 시각화하며, 이상적인 경우인 대각선(완벽한 보정)을 기준으로 모델이 과신하거나 과소신하는 구간을 시각적으로 확인할 수 있도록 한다. 막대는 각 confidence 구간의 실제 정확도를 나타내며, 파란 막대와 회색 대각선 사이의 빨간 음영은 신뢰도 오차를 시각적으로 표현한다. 이 결과를 통해 모델이 얼마나 calibrated 되어 있는지 확인할 수 있고, 이후 보정 기법(예: temperature scaling)의 필요성을 평가하는 기반 자료가 된다.

4. Temperature Scaling 실험

import torch.nn as nn
import os
import matplotlib.pyplot as plt

# Temperature Scaler 정의 (학습 없이 고정된 T 값 사용)
class TemperatureScaler(nn.Module):
    def __init__(self, temperature: float):
        super().__init__()
        self.temperature = nn.Parameter(torch.tensor([temperature]), requires_grad=False)

    def forward(self, logits):
        return logits / self.temperature

# 모델을 Temperature Scaler로 감싸는 래퍼
class WrappedModel(nn.Module):
    def __init__(self, base_model, temp_scaler):
        super().__init__()
        self.base_model = base_model
        self.temp_scaler = temp_scaler

    def forward(self, x):
        logits = self.base_model(x)
        return self.temp_scaler(logits)

# 다양한 T 값에 대해 ECE 계산 및 Reliability Diagram 저장
def evaluate_multiple_temperatures_with_plots(model, test_loader, device, T_values, output_dir):
    os.makedirs(output_dir, exist_ok=True)
    ece_list = []

    for T in T_values:
        print(f"\n🧪 Evaluating T = {T}")
        temp_scaler = TemperatureScaler(temperature=T).to(device)
        wrapped_model = WrappedModel(model, temp_scaler).to(device)

        # 신뢰도 평가
        bin_centers, accs, confs, bin_counts, total_samples, ece = compute_reliability_and_ece(
            wrapped_model, test_loader, device, verbose_under_100=False
        )
        ece_list.append(ece)

        # Reliability Diagram 저장
        draw_fancy_reliability_diagram(
            bin_centers, accs, confs, bin_counts, total_samples, ece,
            name=f"T={T}", output_dir=output_dir
        )

    return T_values, ece_list

# T에 따른 ECE 변화를 시각화
def plot_temperature_vs_ece(T_values, ece_list, save_path):
    plt.figure(figsize=(6, 4))
    plt.plot(T_values, [ece * 100 for ece in ece_list], marker='o', linestyle='-', color='purple')
    plt.xlabel("Temperature (T)")
    plt.ylabel("ECE (%)")
    plt.title("ECE vs Temperature")
    plt.grid(True)
    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()