Colors

계산사진학과 관련된 자료는 포항공과대학교 조성현 교수님의 계산사진학 강의를 기반으로 정리하였으며, 개인적으로 공부한 내용을 포함하고 있습니다.

하늘은 왜 파랗고, 바다는 왜 푸를까? 당연하게 받아들였던 색의 세계를 수학과 공학의 시각에서 바라보고자 한다. 우리가 느끼는 “색”이라는 단어는 지극히 인간적인 감각에 의존한다고 생각할 수 있는데, 카메라와 같은 디지털 세계에서는 어떻게 정의하고, 처리하고, 응용할 수 있는지를 다루어보고자 한다.

🎨 Color Basics

현대의 디지털 이미징과 컴퓨터 비전에서는 색, color를 어떻게 수학적으로 다루고 처리할지를 이해하는것이 필수적이다. 색을 기술하고 사용하는데 필요한 기본적인 개념인 color model과 color space를 우선 살펴보고자 한다.

Color Model

색은 단순한 감정의 대상이 아니라, 수학적으로 정의된 좌표 공간 안에 위치한 하나의 점이다. 색상 모델은 이러한 색을 수치적으로 표현하기 위한 추상적인 수학 모델로, 일반적으로 하나의 좌표계와 그 안에서 실제 색들이 존재하는 하위 공간(subspace)으로 구성된다. 다시 말해, 색상 모델은 어떤 좌표계를 기준으로 색을 어떻게 수치화할지를 정의하고, 그 안에서 실제 색상이 표현될 수 있는 범위를 명시하는 구조를 말한다.

Figure 1: RGB Color Model

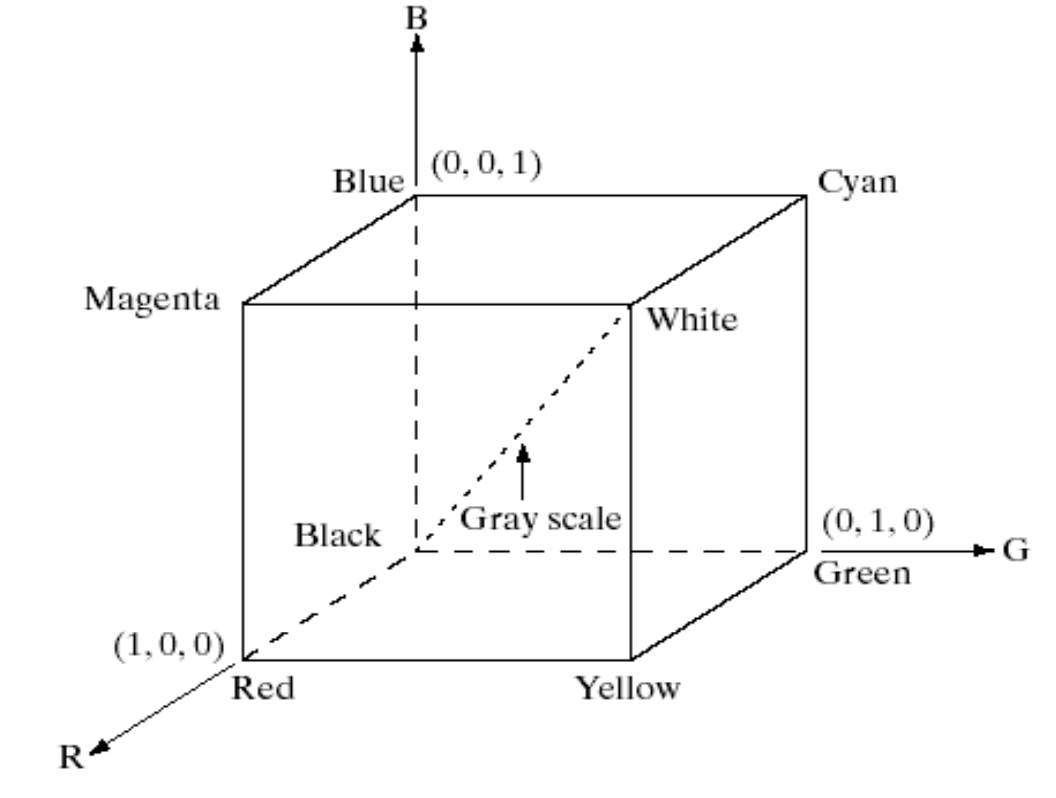
어렵게 설명했지만 Figure 1에서 볼 수 있는 RGB Color Model은 우리에게 친숙한 단어이다. 이외에도 CMK, CMYK, HSV와 같은 다양한 종류의 Color Model이 존재하며 각각을 자세히 살펴보도록 하겠다.

🔴 RGB (Red, Green, Blue)

RGB는 빛의 삼원색인 빨강(R), 초록(G), 파랑(B)을 조합하여 색을 표현하는 모델로, 디스플레이나 카메라 등 빛을 사용하는 장치에서 표준적으로 사용된다. 이 모델은 3차원 직교 좌표계로 구성되어 있으며, 각 축은 R, G, B 값을 0~1 또는 0~255 범위의 실수 혹은 정수로 표현한다. 모든 색은 이 세 색의 가중합으로 구성되며, 예를 들어 (1, 0, 0)은 순수한 빨강을, (1, 1, 1)은 흰색을 나타낸다.

RGB 모델의 강점은 하드웨어 친화성에 있다. 카메라 센서나 모니터는 실제로 RGB 채널로 빛을 감지하거나 방출하기 때문에, 데이터를 수집하고 출력하는 데 매우 효율적이다. 하지만 색상 성분 간의 강한 상관성과 비직관성은 단점으로 작용한다. 예를 들어 사람이 보기에 ‘보라색’이 어떤 RGB 값을 가져야 할지를 직관적으로 알기 어렵다. 이 때문에 색상 편집, 보정, 분석 등의 용도에는 부적합하다.

🟠 CMY / CMYK (Cyan, Magenta, Yellow, Black)

Figure 2: CMY 혼합 다이어그램

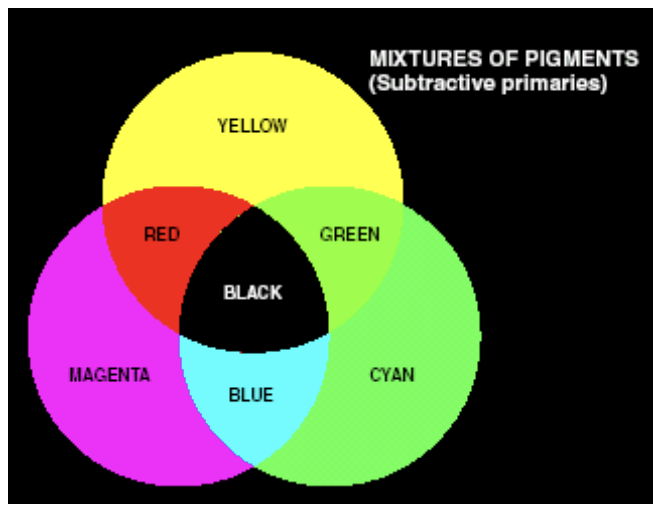
CMY 모델은 RGB와는 반대 개념인 감산 혼합(Subtractive Mixing)에 기반한 색상 모델이다. RGB는 빛을 더해 색을 만드는 방식인 반면, CMY는 빛을 흡수하는 색소의 혼합을 다룬다. 각 색상은 다음과 같이 RGB로부터 변환된다.

\[\begin{bmatrix} C \\ M \\ Y \\ \end{bmatrix} = \begin{bmatrix} 1 - R \\ 1 - G \\ 1 - B \\ \end{bmatrix}\]

이 모델은 잉크나 페인트와 같이 색소 기반의 출력 장치에서 사용되며, 프린터는 일반적으로 CMY 정보를 입력받거나 내부적으로 RGB를 CMY로 변환해 사용한다. 이론적으로 동일한 양의 시안, 마젠타, 옐로우를 섞으면 검정이 나와야 하지만, 실제 색소는 불완전하므로 순수한 검정을 표현하기 어렵다. 이를 보완하기 위해 검정(K, Key) 채널을 추가하여 CMYK 모델이 널리 사용된다. CMYK 모델은 RGB에 비해 인간 시각적 감성보다는 물리적 구현에 초점이 맞추어져 있으며, 색 정확도보다 출력 비용과 효율성이 중요시되는 환경에 적합하다.

🟢 HSI / HSV / HSL (Hue, Saturation, Intensity / Value / Lightness)

RGB나 CMY가 물리적인 장치 중심의 모델이라면, HSI 계열 모델은 인간의 색 인지 과정을 모사한 지각 중심 모델이다. 이 모델들은 색상을 다음 세 가지로 분리하여 표현한다.

• Hue (색상): 색의 종류를 나타내며, 일반적으로 원형 색상환 상의 각도로 표현된다.
• Saturation (채도): 색의 순도를 의미하며, 얼마나 흰색이 섞였는지를 나타낸다.
• Intensity / Value / Lightness (명도): 색의 밝기를 나타내는 요소로, 모델에 따라 수학적 정의가 다르다.

이러한 구조는 색조와 밝기를 분리해서 조작할 수 있게 해 주며, 히스토그램 평활화나 채도 조절 등 색상 편집 작업에 특히 유리하다. HSV와 HSL은 HSI에서 파생된 모델로, 명도 성분(Value 또는 Lightness)을 정의하는 방식이 다르다. 이 모델들의 장점은 색상 편집의 직관성과 유연성에 있으며, 특히 포토샵이나 파이썬 이미지 프로세싱 라이브러리(OpenCV 등)에서 색상 분할, 필터링, 색 보정 작업에 자주 사용된다. 반면, 하드웨어 구현에는 적합하지 않기 때문에 최종 디스플레이 출력 단계에서는 다시 RGB로 변환하는 절차가 필요하다.

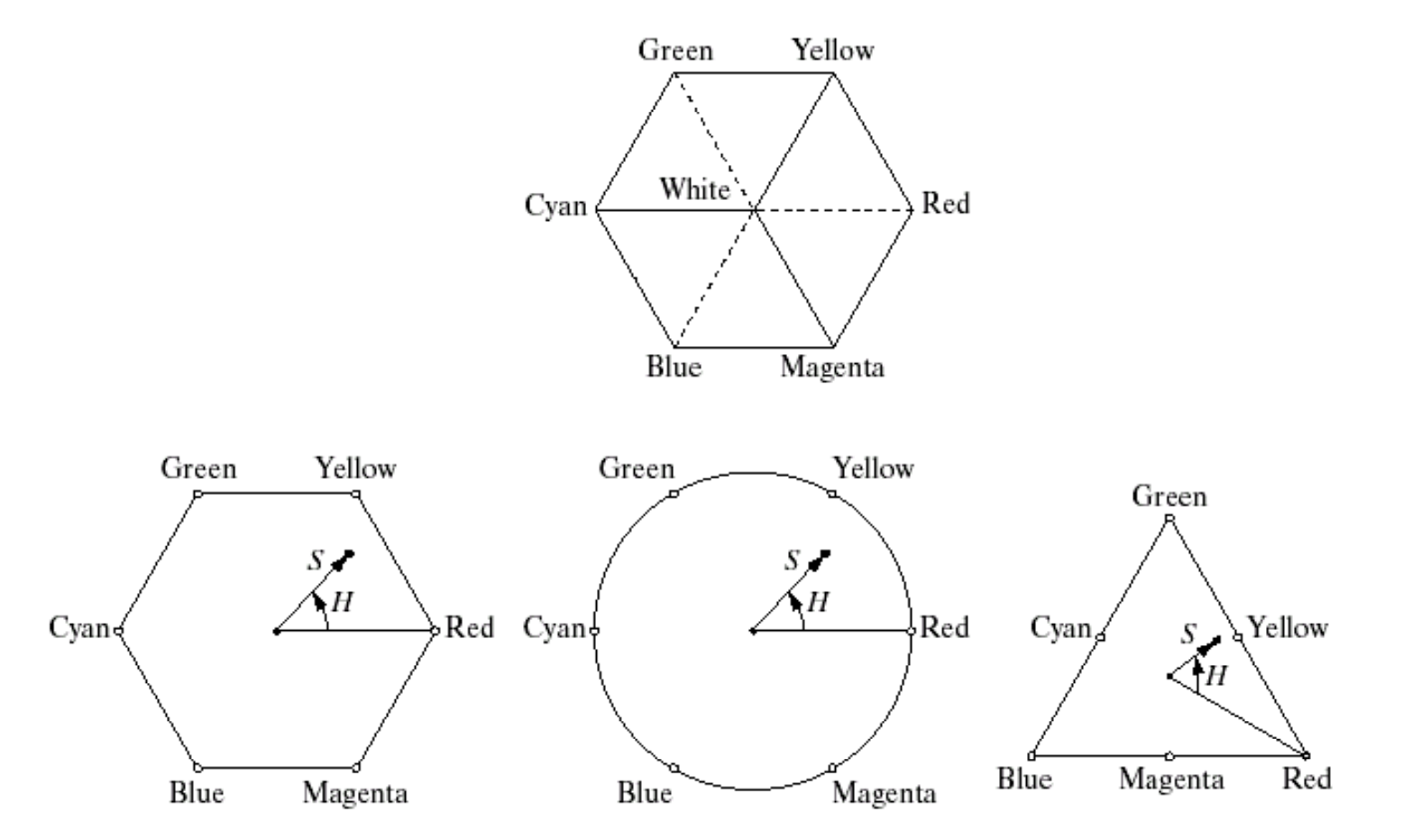
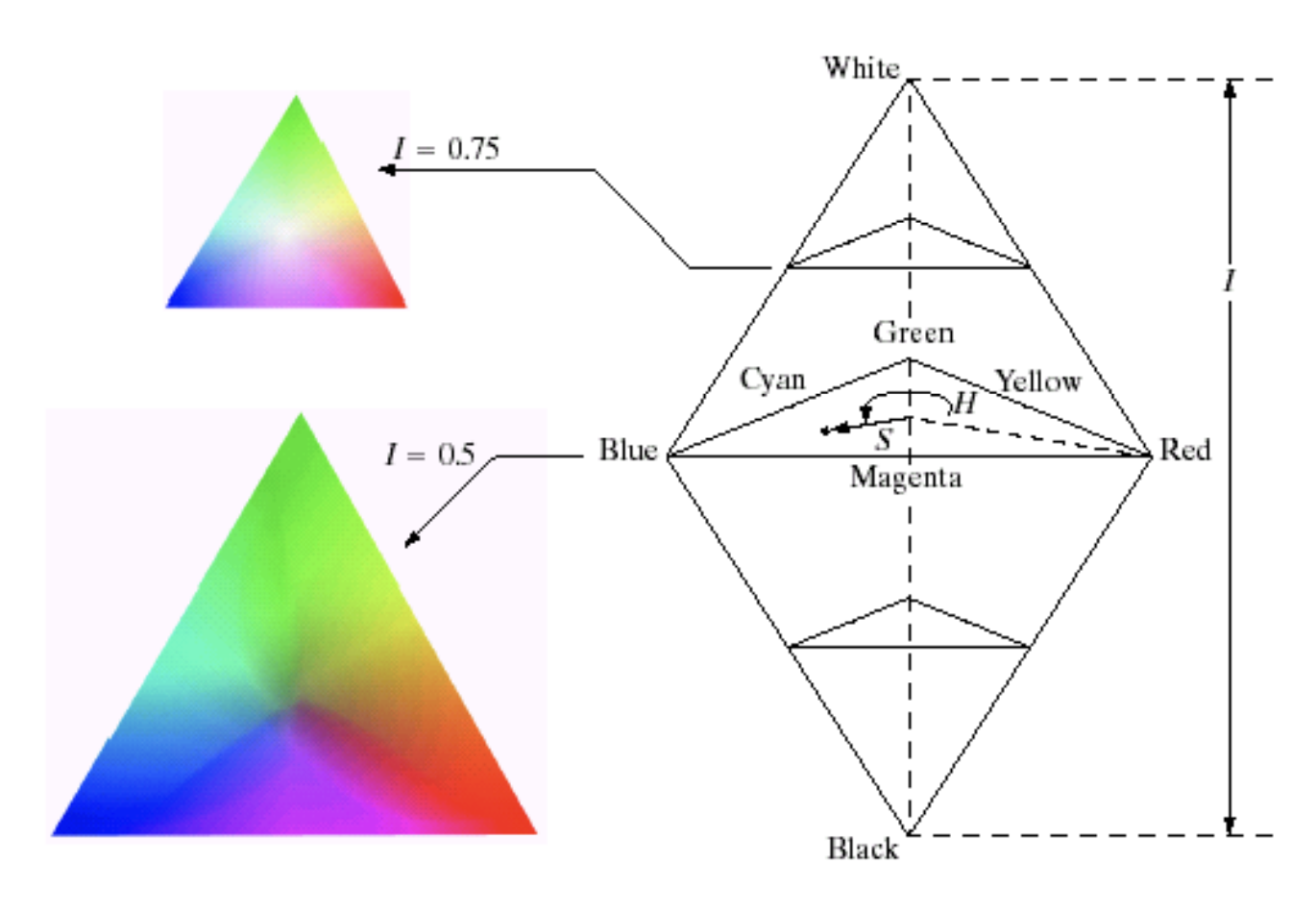Figure 3: HSI 색 공간 구조와 평면 시각화 예시

위 그림은 HSI 색상 모델의 공간 구조를 시각화한 도식으로, 사람의 색 인지 방식에 따라 색상(Hue), 채도(Saturation), 명도(Intensity)가 어떻게 구성되는지를 보여준다. 우측의 다이어그램은 전체 HSI 색 공간의 기하학적 구조를 나타내며, 그림은 정사면체를 두개 붙여놓은 형태를 따르고 있다. 이의 모양은 크게 중요하지 않다. 우선 해당 구조에서 세 성분은 다음과 같은 방식으로 해석된다.

• Hue (H): 원형 평면에서 색상의 각도로 표현된다. 예를 들어, 빨강은 0°, 초록은 120°, 파랑은 240°에 해당한다.
• Saturation (S): 중심축으로부터의 거리로 표현되며, 중심에 가까울수록 채도가 낮고, 외곽으로 갈수록 채도가 높아진다.
• Intensity (I): 수직 축의 높이로 정의되며, 아래는 검정(Black), 위는 흰색(White)에 해당한다.

좌측의 삼각형 이미지는 각각 특정 명도를 기준으로 H와 S 성분을 시각화한 단면이다.

• 위쪽 평면은 ( I = 0.75 )일 때의 색상 분포를 보여주며, 더 밝은 색들이 많이 포함되어 있다.
• 아래쪽 평면은 ( I = 0.5 )일 때의 분포로, 어두운 계열의 색이 중심에 더 가깝게 나타난다.

이와 같이 HSI 공간에서는 밝기와 색조, 순도를 완전히 분리하여 다룰 수 있기 때문에, 명도만 조절하거나 색조만 선택적으로 변형하는 색상 처리에서 압도적인 직관성과 제어력을 제공한다. 더불어 Figure 3은 정사면체 두개를 붙여 놓은 형태로 나타내었는데, 원뿔을 붙여놓기도 다양한 방법으로 표현이 가능하고 단면의 모든 지점에서 I가 같다는 것이 중요하다. 아래와 같이 다양한 모양으로 표현이 가능하며 이 때 단면에서 계산가능한 S와 H는 그림과 같이 나타난다.

Figure 4: HSI 색 공간의 평면 구조 예시

🔁 RGB → HSI 변환 수식

지금부터는 우리가 가장 많이 활용하는 RGB 값을 어떻게 HSI로 변환가능한지 살펴보도록 하겠다.

1. Intensity (명도)
RGB의 평균값으로 정의되며, 전체적인 밝기를 나타낸다.

\[I = \frac{R + G + B}{3}\]

2. Saturation (채도)
색의 순도이며, 흰색이 얼마나 섞였는지를 의미한다:

\[S = 1 - \frac{3}{R + G + B}\]

3. Hue (색조)
색의 종류를 각도로 표현하며, 다음과 같이 계산된다. 먼저 각도를 계산할 중간 단계 변수 \(\theta\)를 정의한다.

\[\theta = \cos^{-1} \left( \frac{ \frac{1}{2}[(R - G) + (R - B)] }{ \sqrt{(R - G)^2 + (R - B)(G - B)} } \right)\]

Hue는 다음과 같이 정의된다.

\[H = \begin{cases} \theta, & \text{if } B \leq G \\ 360^\circ - \theta, & \text{if } B > G \end{cases}\]

🔁 HSI → RGB 변환

반대로 HSI에서 RGB로 변환하려면 Hue 각도를 기준으로 다음 세 가지 영역으로 나누어 계산한다.

• RG 영역: \(0^\circ \leq H < 120^\circ\)
• GB 영역: \(120^\circ \leq H < 240^\circ\)
• BR 영역: \(240^\circ \leq H < 360^\circ\)

각 영역마다 R, G, B의 계산 방식이 다르며, 이들은 수치적 근사 방식으로 구현되는 경우가 많다. 따라서 HSI에서 RGB로의 변환은 다소 복잡한 삼각함수 연산을 수반하게 된다.

🟣 YCbCr (Luma + Chroma 기반 색상 모델)

YCbCr 색상 모델은 영상 압축과 전송에 최적화된 컬러 모델로, JPEG 이미지와 MPEG, H.264 같은 비디오 코덱에서 표준적으로 사용된다. RGB와 같은 장치 중심 모델과 달리, 시각적 지각 특성을 반영하여 색상 정보를 분리하고 효율적으로 표현한다. YCbCr은 다음 세 가지 구성 요소로 이루어진다.

• Y (Luma): 밝기 성분으로, 흑백 정보에 해당하며 인간의 눈이 가장 민감하게 반응하는 요소이다.
• Cb (Chroma Blue): 파란색과 밝기 성분의 차이로, 색상 정보 중 파란색 계열을 나타낸다.
• Cr (Chroma Red): 빨간색과 밝기 성분의 차이로, 색상 정보 중 빨간색 계열을 나타낸다.

사람의 눈은 색상보다는 밝기에 더 민감하다. 이를 활용하여 밝기 정보(Y)는 고해상도로 유지하고, 색상 정보(Cb, Cr)는 저해상도로 샘플링한다. 이 방식은 Chroma Subsampling이라 불리며, 다음과 같은 유형이 존재한다.

• 4:4:4 : 모든 픽셀에 대해 Y, Cb, Cr 값을 유지 (무손실)
• 4:2:2 : 수평 해상도 기준으로 Cb, Cr 값을 절반만 유지
• 4:2:0 : 수평과 수직 모두 절반 해상도로 Cb, Cr 값을 유지

이로 인해 색상 정보의 용량을 줄이면서도 시각적으로는 품질 저하가 거의 없는 효율적인 영상 압축이 가능하다. 이는 JPEG 이미지 인코딩, 디지털 TV 방송, H.264/AVC 등의 비디오 인코딩 등에 활용된다. YCbCr은 밝기와 색상을 분리해 저장 효율을 극대화하고, 시각적 품질 손실 없이 데이터 용량을 줄일 수 있는 핵심 모델로 자리잡고 있다.

지금까지 다양한 구조의 Color Model을 살펴보았다. 각 색상 모델은 고유한 목적과 사용 환경에 맞게 설계되며, 색상 데이터를 어떻게 해석하고 활용할지에 따라 적절한 모델을 선택하는 것이 중요함을 확인할 수 있었다. 이러한 개념을 바탕으로, 이제부터는 색상 모델을 기반으로 실제 색이 어떻게 정의되고 구현되는지를 결정하는 Color Space의 개념을 살펴보고자 한다.

Color Space

앞서 소개한 RGB, CMY, HSI 등은 색을 수학적으로 좌표화하는 모델이다. 그러나 이 모델들만으로는 해당 좌표가 정확히 어떤 물리적 색상을 의미하는지 알 수 없다. 여기서 Color Space(색 공간)가 등장한다. Color Space는 특정 색상 모델 위에 정의된 매핑 함수(mapping function)를 포함하는 개념으로, 수학적 좌표가 실질적으로 어떤 색을 나타내는지를 결정한다.

예를 들어, RGB 모델에서 (255, 0, 0)이라는 좌표는 단순히 “최대의 빨강”을 의미하는 숫자일 뿐이다. 하지만 이 값이 sRGB에서 정의된 것인지, 아니면 AdobeRGB나 다른 색 공간에서 정의된 것인지에 따라 실제로 표현되는 빨강의 색조와 채도는 달라진다. 다시 말해, 동일한 RGB 좌표라도 어떤 Color Space에 속해 있느냐에 따라 서로 다른 색의 범위(gamut)를 가지게 된다.

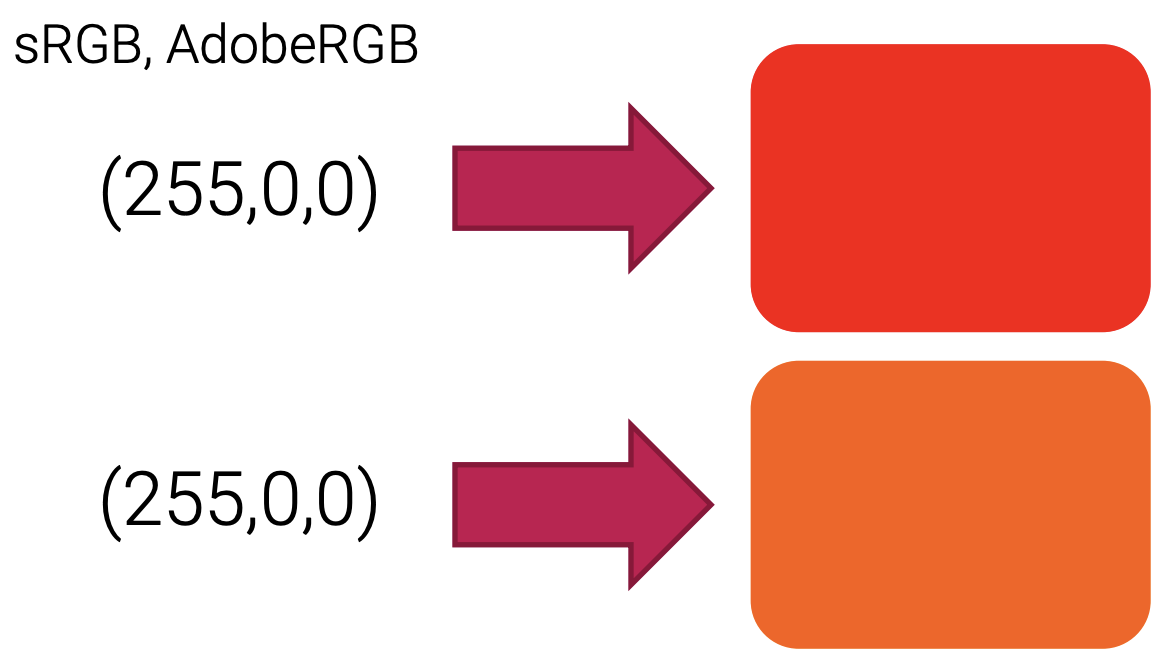Figure 5: RGB 기반 Color Space의 비교 – sRGB vs AdobeRGB

위 그림은 대표적인 두 RGB 기반 색 공간인 sRGB와 AdobeRGB를 비교한 것이다. 두 Color Space 모두 동일한 RGB 모델을 기반으로 하지만, 각 채널이 매핑하는 실제 색상의 범위는 다르다. AdobeRGB는 더 넓은 색 영역을 표현할 수 있도록 설계되어 있는 반면, sRGB는 대부분의 디스플레이와 웹 콘텐츠에 최적화되어 있다. 이처럼 색상 모델만으로는 색의 정량적 정의가 불완전하며, 그 위에 정의된 색 공간 정보가 함께 주어져야 비로소 정확한 색 표현이 가능하다. 따라서 디지털 이미지 처리에서는 각 픽셀의 값뿐 아니라, 그것이 어떤 색 공간에 속하는지를 함께 고려해야 한다. 실제로는 색상 모델과 색 공간을 구분하지 않고 혼용하는 경우도 많지만, 고품질 색상 보정이나 디바이스 간 일관된 색 재현이 요구되는 작업에서는 이 둘을 명확히 구분하는 것이 필수적이다.

CIELAB Color Space

Color Space의 개념이 발전함에 따라, 단순히 장치에 의존하지 않고 사람의 지각에 기반한 색 공간이 필요하게 되었다. 이러한 필요로부터 등장한 것이 바로 CIELAB 색 공간이다. CIELAB은 1976년 국제조명위원회(CIE)가 정의한 색 공간으로, 인간이 인지하는 색상의 차이를 수학적으로 정량화할 수 있도록 설계되었다.

CIELAB 색 공간은 다음과 같은 세 축으로 구성된다.

• L (Lightness): 밝기를 나타내며, 0은 검정, 100은 백색에 해당한다.
• a: 초록(Green, 음수)과 빨강(Red, 양수) 축을 따라 색상 차이를 나타낸다.
• b: 파랑(Blue, 음수)과 노랑(Yellow, 양수) 축을 따라 색상 차이를 나타낸다.

이 구조는 지각적으로 균일한(perceptually uniform) 색 공간을 목표로 한다. 즉, CIELAB 공간에서 두 점 사이의 유클리드 거리(Euclidean distance)는 인간이 느끼는 색상 차이와 잘 일치하도록 설계되었다.

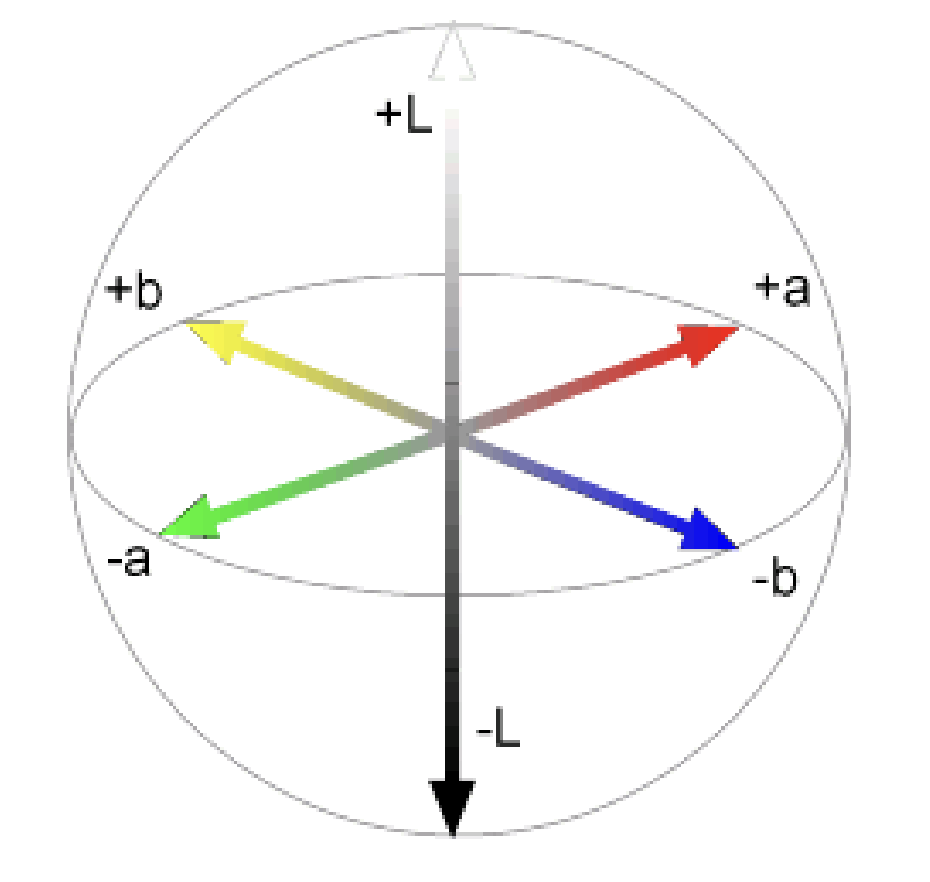Figure 6: CIELAB color space 구조

• L 축은 수직 방향으로 밝기를,
• a-b 평면은 색상의 방향성과 대비를 표현한다.

CIELAB의 가장 큰 장점은 디바이스 독립성(device-independence)에 있다. 어떤 장치에서도 동일한 CIELAB 값은 동일한 색 지각을 유도하는 이론적 기반을 제공한다. 이 때문에 CIELAB은 색 정확성이 중요한 인쇄, 색상 교정, 의료 영상, 컬러 매칭 등의 분야에서 널리 사용된다.

Color Image Processing

Color Image Processing은 단순한 픽셀 단위의 계산을 넘어, 색상(Hue), 채도(Saturation), 명도(Intensity) 등을 고려하여 더욱 정교하고 지각 기반의 처리를 가능하게 한다. 컬러 정보는 RGB 형태로 표현될 수 있지만, 시각적 의미를 반영하려면 HSI 또는 다른 색상 공간으로의 변환이 자주 활용되며 지금부터는 대표적인 컬러 이미지 처리 기법들을 알아보고자 한다.

Chroma Subsampling

Chroma Subsampling은 주로 영상 압축(video compression)이나 전송(video transmission)에서 사용되는 중요한 기법으로, 밝기(brightness, 또는 luminance) 성분은 그대로 유지하면서, 색상 정보(chroma)의 해상도를 낮추어 데이터의 전체 크기를 줄이는 방법이다. 이는 인간 시각 시스템의 특성을 기반으로 설계되었으며, 사람의 눈은 밝기 정보에는 매우 민감하게 반응하지만, 색상 정보에는 비교적 둔감하게 반응한다. 이러한 지각 기반 특성을 활용하면, 색상 데이터를 일부 손실시키더라도 전체 이미지의 시각적 품질에는 거의 영향을 주지 않으면서 데이터 양을 효과적으로 줄일 수 있다.

📐 기본 아이디어

Chroma Subsampling은 보통 YCbCr 또는 YUV와 같은 컬러 모델을 기반으로 적용된다. 이러한 모델들은 색 정보를 다음과 같이 분리한다.

• Y (Luminance): 밝기 정보
• Cb/Cr (Chrominance): 색상 정보 (파랑-밝기, 빨강-밝기 차이)

예를 들어, 8개의 픽셀이 있다고 할 때, 각 픽셀은 하나의 Y (밝기)와 하나의 Cb/Cr (색상)을 가질 수 있다. 이를 4:4:4 방식이라 한다. 그러나 색상에 덜 민감하다는 전제하에, 모든 픽셀에 색상 정보를 개별적으로 저장할 필요는 없다.

대표적인 Subsampling 형식은 다음과 같다. 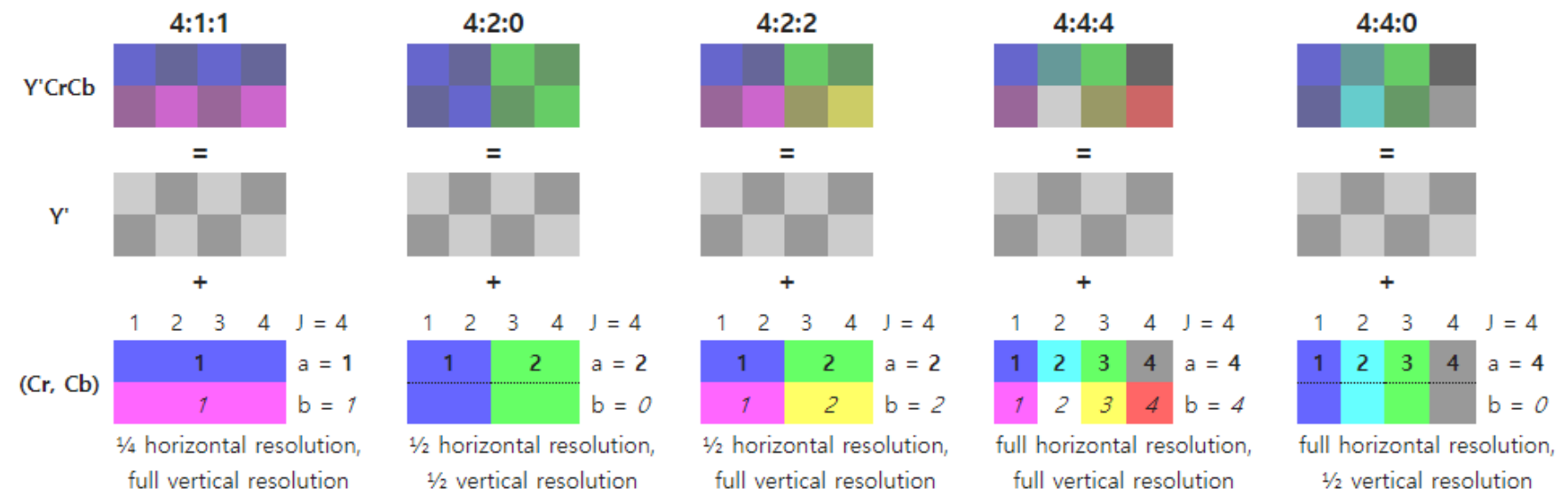Figure 7: Chroma Subsampling 예시

1. 4:4:4
   • Y, Cb, Cr 모두 1:1로 저장
   • 가장 고해상도이며, 색 손실 없음
   • 데이터 크기 가장 큼
2. 4:2:2
   • Y는 4픽셀마다 4개 저장, Cb와 Cr은 각각 2개 저장
   • 수평 방향 해상도만 절반으로 줄임
   • 시각적으로 거의 차이 없음
3. 4:1:1
   • Y는 4개, Cb와 Cr은 각각 1개만 저장
   • 4개의 픽셀이 같은 색상 정보를 공유함
   • 더 높은 압축률
4. 4:2:0
   • 수평과 수직 모두 색 해상도를 절반으로 줄임
   • JPEG, MPEG, H.264 등 대부분의 영상 압축 포맷에서 사용됨

🎨 Color Image Editing

컬러 이미지는 HSI 모델로 변환함으로써 색상 성분을 개별적으로 조작할 수 있다.

• Saturation 조절: 색의 선명도를 조절하여 이미지의 생동감을 변경할 수 있음
• Hue 조절: 색조 자체를 회전시켜 색상의 전체적인 분위기를 바꿀 수 있음
• Intensity 조절: 전체적인 밝기를 조절할 수 있음

이러한 조작은 RGB 공간에서 직접 수행하기보다, HSI 공간에서 더 직관적으로 이루어진다.

🟣 Histogram Equalization for Color Images

컬러 이미지에 히스토그램 평활화를 적용할 때는 색상 왜곡(color distortion)을 피하는 것이 중요하다. 대표적인 두 가지 방식이 존재한다.

1. Per-Channel Method (RGB 또는 CMY 채널별)
   • 각 채널(R, G, B)을 독립적으로 히스토그램 평활화한 뒤 다시 합성
   • 색 왜곡이 발생할 수 있음
2. HSI Intensity-Based Method
   • HSI로 변환한 뒤, 명도(Intensity) 채널만 평활화하고 H, S는 유지
   • 색조 보존에 유리함

히스토그램 평활화는 다음 수식을 기반으로 이루어진다.

\[s_k = T(r_k) = (L - 1) \sum_{j=0}^{k} \frac{n_j}{N}\]

여기서 \(r_k\)는 입력 이미지의 intensity 값, \(s_k\)는 출력 이미지의 평활화된 intensity 값이며, \(L\)은 intensity의 총 단계 수, \(n_j\)는 \(r_j\)의 빈도수, \(N\)은 전체 픽셀 수이다.

🧼 Color Image Smoothing

컬러 이미지에서 노이즈 제거(smoothing)를 수행할 때도 두 가지 접근 방식이 있다.

1. RGB 채널별 필터링
   • R, G, B 채널 각각에 스무딩 필터(예: 평균, 가우시안)를 적용
   • 다시 합쳐서 출력 이미지 구성
   • 처리 간에 채널 간 정보 손실 가능
2. HSI에서 I 채널만 필터링
   • 색조(H)와 채도(S)는 유지하면서, 밝기(I)만 부드럽게 처리
   • 시각적으로 더 자연스러운 결과를 생성함

Figure 8: Color Image Smoothing 예시

두 방법은 결과적으로 서로 다른 이미지를 생성하며, 후자의 방식이 속도와 색상 보존 측면에서 더 유리하다.

✴️ Color Image Sharpening

스무딩과 반대로, 컬러 이미지를 선명하게(sharpening) 만들기 위한 방식도 존재한다.

1. RGB 채널별로 샤프닝 필터 적용
2. HSI에서 I 채널만 강조

두 방식의 차이는 스무딩 때와 동일하며, 색상 유지가 중요한 경우 HSI에서의 Intensity 조절 방식이 더 선호된다.

---

More About Colors

색은 물리적 실체가 아니라 지각(perception)이다

지금까지 우리가 색, Color에 대해서 다루어 보았다. 이것이 물리적인 속성인가라고 생각을 해보면 그렇지 않다는 것이다. “색은 물리적 속성이 아니라, 감각이다.”라는 것이다. 빨강, 초록, 파랑, 심지어 ‘Atomic Tangerine’이나 ‘Baby Pink’ 같은 미묘한 색상 명칭은 실제로 존재하는 고정된 물리량이 아니라, 우리가 눈과 뇌를 통해 느끼는 감각의 언어이다. 즉, 색이란 ‘객관적 실재’라기보다, 우리의 신경 시스템이 빛을 해석한 결과라고 볼 수 있다.

주관적인 색의 구성 요소

우리가 앞서 살펴보았듯이 색을 설명할 때 사용하는 용어들은 대부분 주관적인 지각에 기반한다.

• Hue (색상): 노랑, 빨강, 파랑처럼 색의 종류를 나타냄
• Saturation, Chroma (채도): 색의 강도, 순도. 얼마나 선명한가?
• Brightness, Value (명도): 색이 얼마나 밝거나 어두운가?

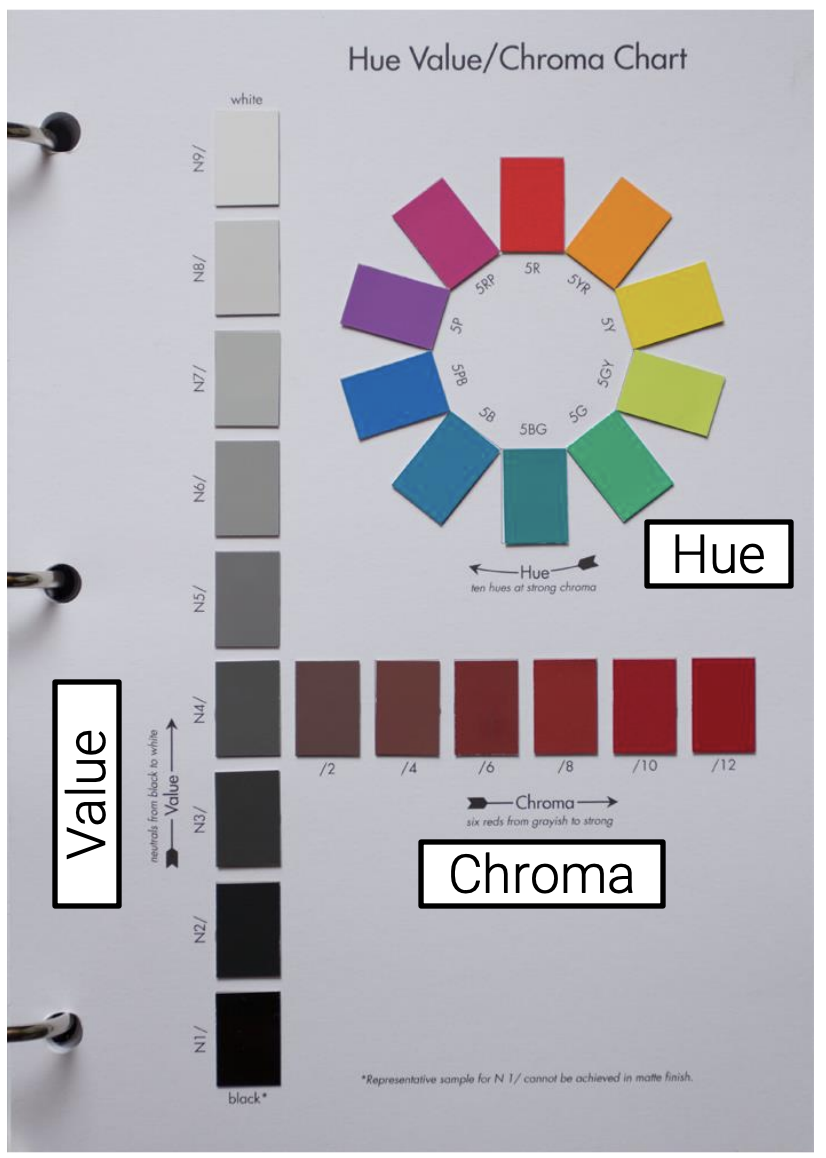Figure 9: Hue, Value, Chroma 그림

색 자극은 어디서 오는가?

색은 전자기파의 반사와 흡수에서 비롯된다. 사람의 눈은 약 390~700nm의 파장을 가진 빛만을 볼 수 있으며, 이 범위가 우리가 말하는 가시광선(visible spectrum)이다. 그리고 백색광(White light)은 여러 파장의 빛으로 구성되어 있으며, 프리즘을 통과시키면 파장에 따라 굴절률이 달라져 무지개처럼 퍼지게 된다.

인간 눈의 구조와 색 지각

인간의 눈은 보이는 전자기파를 포착하게 되고, 복잡한 과정을 거쳐 물체를 인식하게 된다. 즉, 하나의 정교한 카메라처럼 작동하게 되는 것이며 아래와 같이 구성되어져 있다.

• 홍채(iris)는 조리개 역할을 하며, 빛의 양을 조절한다.
• 망막(retina)에는 두 종류의 빛 수용체가 존재한다:
  • 막대세포(Rods): 밝기 감지, 주로 야간에 작동, 흑백 시야 제공
  • 원뿔세포(Cones): 색상 감지, 밝은 환경에서 작동, 3종류 존재
    • R (적색), G (녹색), B (청색) 영역에 각각 민감

Tristimulus Color Theory (삼자극 이론)

인간 눈이 색을 인식하는 과정은 3종류의 원뿔세포를 기반으로 한다는 사실에 기반해, 삼자극 이론(tristimulus theory)이 정립되었다.

해당 이론에 따르면

• 인간은 단 세 가지 기본 자극(R, G, B)의 조합만으로 모든 색을 인지할 수 있다.
• 실제로 서로 다른 스펙트럼 분포(SPD)를 가지는 빛이라도, 3자극 값이 같으면 같은 색으로 지각된다.

이를 통해 색 공간을 단순화할 수 있는 가능성이 생기며, 이후 CIE XYZ와 같은 표준 색 공간이 개발되는 기반이 된다.

SPD(Spectral Power Distribution)와 지각의 모호성

앞서 ‘SPD가 다르다.’라고 했는데 SPD, Spectral Power Distribution이 무엇일까? 현실에서 우리가 보는 대부분의 색은 단일 파장의 빛이 아닌, 다양한 파장의 빛이 혼합된 결과이다. 이러한 빛의 구성 성분을 파장에 따라 정량적으로 표현한 것이 바로 SPD(Spectral Power Distribution)이다. SPD는 특정 광원이나 물체가 반사하는 빛의 파장별 세기를 그래프로 나타낸 것으로, x축은 파장(보통 390~700nm), y축은 해당 파장에서의 상대 에너지 값이다. 이러한 SPD는 현실 세계의 색을 나타내는 물리적 표현으로, 자연광, 형광등, LED 등 각기 다른 조명은 고유의 SPD를 가지게 된다. 또한, 물체는 외부 광원을 반사할 때 파장별 반사율이 달라 각기 다른 SPD를 형성하게 되고, 결과적으로 어떤 물체를 본다는 것은 조명 SPD × 물체 반사율이라는 조합을 눈이 받아들이는 것이다.

그러나 서로 다른 SPD를 가진 빛이라 하더라도, 인간의 시각 시스템이 그것을 동일한 색상으로 지각할 수 있다. 이러한 모호성 때문에, 물리적으로 완전히 다른 빛이 심리적으로는 같은 색으로 보이는 현상이 생긴다. 쉽게 밀해 SPD는 다차원적(continuous)인 색 정보의 물리적 표현이며, 인간은 이를 단지 세 개의 숫자(R, G, B 자극)로 요약해 받아들이면서 사람이 구분하지 못하는 경우가 발생하기도 하는 것이다.

---

Radiometry vs. Photometry

앞서 살펴본 삼자극 이론(Tristimulus Color Theory) 덕분에, 우리는 특정한 색을 기본 색(primary color)의 선형 조합으로 표현할 수 있게 되었다. 하지만 이때 한 가지 중요한 질문이 생긴다.

“이러한 색을 어떻게 수치적으로, 그리고 객관적으로 표현할 수 있을까?”

이를 위해서는 단순히 색의 조합만이 아니라, 빛의 양(에너지) 자체를 정량적으로 측정할 수 있는 체계가 필요하다. 색은 결국 빛의 일종이기 때문에, 광의 물리적 특성을 정의하고 측정하는 체계가 중요하다.

이러한 배경에서 두 가지 주요 측정 체계가 등장한다.

• Radiometry (복사 측정)
  전자기 복사의 물리적 에너지를 절대적인 단위로 측정하는 체계이다. 파장에 관계없이 모든 빛 에너지를 동일하게 다룬다.

• Photometry (광도 측정)
  인간의 눈이 인지하는 가시광선 범위 내에서의 밝기를 기준으로 하는 측정 체계이다. 파장에 따라 인간 눈의 민감도를 고려해 측정한다.

이 두 체계를 바탕으로, 우리는 색을 단지 감각이 아닌 정량적 수치로 표현하고 분석할 수 있게 되었으며, 이는 색채 과학(Colorimetry)의 핵심 기반이 된다.

CIE XYZ Color Space

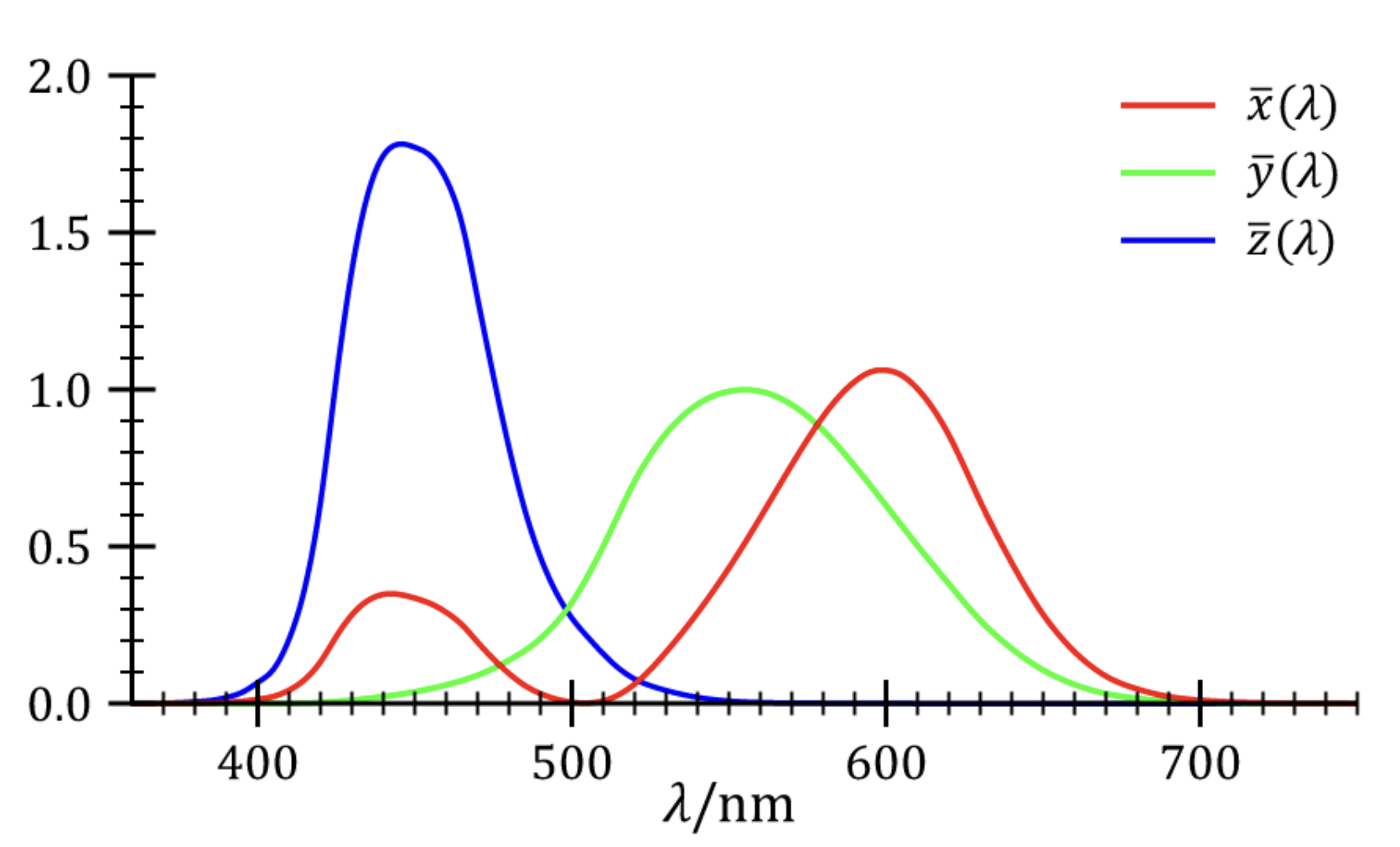
색을 정량적으로 표현하기 위한 여러 시도가 있었지만, 1931년 국제조명위원회(CIE: Commission Internationale de l’Éclairage)는 표준 색상 공간인 CIE XYZ를 제안하였다. 이는 삼자극 이론을 바탕으로 하되, 실제 측정값을 보정하여 모든 가시색을 양수로 표현할 수 있도록 설계된 수학적 색 공간이다.

CIE XYZ는 다음과 같은 특징을 갖는다.

• 인간 시각의 평균 응답을 기반으로 한다 (표준 관찰자).
• 세 가지 가상의 기본 색 자극인 X, Y, Z를 사용한다.
• Y 성분은 밝기(luminance)를 직접 나타낸다.
• X, Y, Z는 실제 물리적 색은 아니지만, 모든 색을 양의 값으로 표현할 수 있도록 구성되어 있다.

\[X = \int_{\lambda} S(\lambda) \cdot \overline{x}(\lambda) \, d\lambda \\ Y = \int_{\lambda} S(\lambda) \cdot \overline{y}(\lambda) \, d\lambda \\ Z = \int_{\lambda} S(\lambda) \cdot \overline{z}(\lambda) \, d\lambda\]

여기서

• ( S(\lambda) ): 광원의 SPD
• ( \overline{x}(\lambda), \overline{y}(\lambda), \overline{z}(\lambda) ): CIE 표준 관찰자 함수
• ( \lambda ): 파장

CIE XYZ 색 공간은 이후의 다양한 색 공간(CIELAB, CIELUV 등)과 색상 비교 지표(ΔE, 색차 등)의 기초가 되었으며, 표준 색 비교와 색 측정의 기준으로 현재까지도 널리 사용된다.

Figure 10: CIE 1931 XYZ 색 공간

CIE XYZ는 단순히 색을 표현하는 것뿐만 아니라, 색상의 정량적 분석, 디스플레이 및 인쇄 장치의 색 보정, 색 차이 평가 등 매우 다양한 응용 분야에서 핵심적인 역할을 하고 있다.