Cameras & Optics
계산사진학과 관련된 자료는 포항공과대학교 조성현 교수님의 계산사진학 강의를 기반으로 정리하였으며, 개인적으로 공부한 내용을 포함하고 있습니다.
카메라는 우리 일상에서 가장 익숙한 기술 중 하나이다. 우리는 스마트폰이나 디지털 카메라를 통해 손쉽게 이미지를 촬영하고 공유할 수 있지만, 그 안에서 실제로 어떤 광학적 원리와 구조가 작동하는지는 쉽게 간과되곤 하며, 전문 사진가들은 단순히 셔터를 누르는 것 이상의 과정을 이해하며 촬영을 진행하게 된다. 그들은 빛의 조건, 피사체의 거리, 렌즈의 특성, 노출 설정 등 외부적인 요소와 함께, 카메라 내부 구조와 광학적 원리에 대한 깊은 이해를 바탕으로 원하는 이미지를 만들어내는 것이다.
본 강의는 특히 카메라의 내부적인 메커니즘에 집중하고자 한다. 카메라가 어떻게 구성되어 있으며, 각 구성 요소를 어떻게 조절하면 이미지에 어떤 변화가 발생하는지 단계별로 살펴볼 것이다. 이를 통해 단순한 사용자를 넘어, 이미지 생성의 원리를 이해하는 사용자로 나아가는 기초를 마련하고자 한다.
📸 DSLR vs Mirrorless Camera vs SLR
카메라의 발전에 따라 이미지 촬영 방식도 다양해졌으며, 최근에는 스마트폰 카메라의 성능도 중요한 문제로 떠오르고 있다. 전통적인 카메라에 한정지어서 생각해보면 우리가 흔히 사용하는 DSLR, 전통적인 SLR, 그리고 최근 각광받는 Mirrorless 카메라는 내부 구조와 빛이 어떤 경로를 통해 움직이는지 등 중요한 차이를 보인다. 이들 각각의 차이를 간단히 비교해보도록 하겠다.
📷 DSLR (Digital Single-Lens Reflex) 카메라
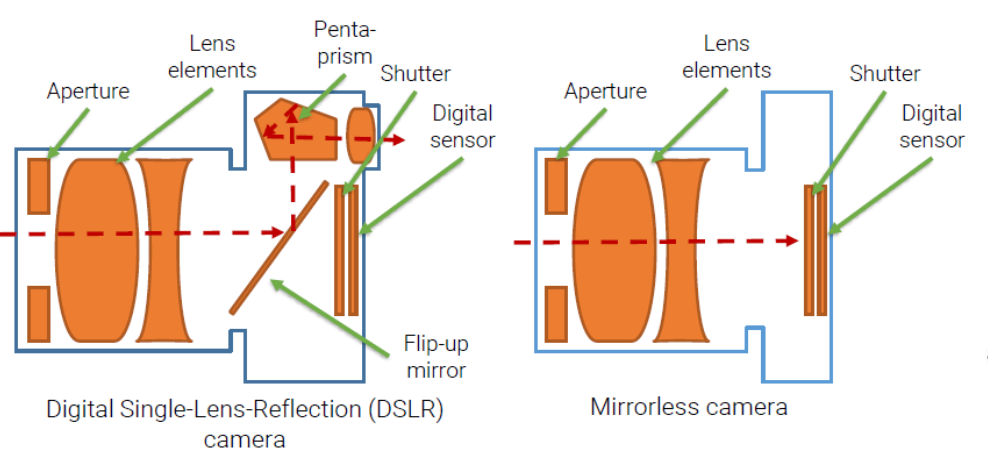Figure 1: DSLR 카메라와 Mirrorless 카메라 모식도
위 Figure 1의 왼쪽 구조는 DSLR 카메라를 보여주고 있다. DSLR은 하나의 렌즈를 통해 빛을 받아들이고, 반사경(mirror)과 펜타프리즘(pentaprism)을 통해 뷰파인더로 광 경로를 유도합니다.
- Aperture: 빛의 양을 조절
- Lens elements: 빛을 모아 이미지 평면으로 전달
- Flip-up Mirror: 평소에는 뷰파인더로 빛을 반사시키지만, 셔터를 누르면 위로 젖혀짐
- Pentaprism: 들어온 빛을 수직으로 반사시켜 뷰파인더로 전달
- Shutter: 셔터가 열리면 빛이 디지털 센서에 도달
- Digital Sensor: 이미지를 디지털 신호로 변환
📝 작동 과정 요약
- 뷰파인더를 통해 장면을 볼 때 → 렌즈 → 미러 → 펜타프리즘 → 눈
- 셔터를 누르면 미러가 위로 젖혀지고 → 셔터 열림 → 센서에 빛이 도달 → 이미지 저장
📱 Mirrorless 카메라
Figure 1의 오른쪽 그림은 Mirrorless 카메라의 구조를 나타낸 것으로, 이름에서도 알 수 있듯이 DSLR에는 존재했던 거울, 미러가 존재하지 않는다.
즉, 광경로가 단순화되어 렌즈 → 조리개 → 센서로 곧바로 연결된다.
- Mirror가 없기 때문에 미러의 움직임으로 인한 시간 지연이나 진동이 없음
- 뷰파인더는 전자식(EVF)을 사용하거나, LCD 화면으로 직접 장면 확인
- 전체 구조가 작고 가벼워지는 장점이 있음
📝 작동 과정 요약
- 렌즈를 통해 들어온 빛이 조리개와 셔터를 통과해 바로 센서로 도달
- 전자식 뷰파인더나 화면을 통해 실시간으로 장면 확인 가능
🎞️ SLR (Single-Lens Reflex) 카메라
DSLR의 전신인 SLR은 구조적으로 거의 동일하지만, 차이점은 이미지 센서가 없고 필름(film)을 사용한다는 점이다.
- 동일한 방식으로 미러와 펜타프리즘을 이용하여 광 경로를 구성
- 셔터가 열리면 디지털 센서 대신 필름에 이미지가 기록됨
📊 요약 비교
| 항목 | SLR | DSLR | Mirrorless |
|---|---|---|---|
| 이미지 저장 방식 | 필름 | 디지털 센서 | 디지털 센서 |
| 미러 존재 여부 | 있음 | 있음 | 없음 |
| 뷰파인더 종류 | 광학식(OVF) | 광학식(OVF) | 전자식(EVF) 또는 LCD |
| 구조 복잡성 | 중간 | 복잡함 | 단순함 |
| 무게 및 크기 | 크고 무거움 | 크고 무거움 | 작고 가벼움 |
| 촬영 지연 시간 | 미러 작동으로 약간 존재 | 미러 작동으로 약간 존재 | 미러가 없어 빠름 |
📷 Camera Structure
앞서 우리가 흔히 사용하는 디지털 카메라의 특징들을 간단하게 살펴보았다. 앞선 그림에서도 확인할 수 있었듯이 카메라는 기본적으로 세 가지 주요 구성요소로 구성된다. 렌즈, 조리개(Aperture), 셔터, 그리고 센서이며 아래와 같이 각각의 구성요소를 정리해볼 수 있을 것이다.
- Lens(렌즈): 외부에서 들어오는 빛을 모아서 이미지 센서 위에 맺히게 한다.
- Aperture(조리개): 빛의 양을 조절한다. 조리개의 크기에 따라 이미지의 밝기와 심도가 달라진다.
- Shutter(셔터): 센서가 빛을 받아들이는 시간을 결정한다.
- Sensor(이미지 센서): 받아들인 빛을 디지털 신호로 변환하여 이미지를 생성한다.
이러한 카메라는 단지 기계적인 장치가 아니라, 인간의 눈의 구조와 기능을 본떠 설계된 광학 시스템이다. 우리가 세상을 인식하는 방식—빛이 눈의 각막과 수정체를 통과해 망막에 맺히는 방식—은 카메라의 렌즈, 조리개, 이미지 센서와 비슷한 구조를 하고 있다고 생각해볼 수 있다.
| 요소 | 카메라 | 인간의 눈 |
|---|---|---|
| 렌즈 | Optical lens | Cornea + Lens |
| 조리개 | Aperture | Pupil |
| 이미지 센서 | CMOS/CCD | Retina |
| 셔터 | Shutter | Eyelid (X) |
📌 Pinhole Camera
그럼 가장 처음 개발된 카메라는 어떤 형태일까? 핀홀 카메라(pinhole camera)는 카메라 역사상 가장 처음 고안된, 가장 단순한 형태의 카메라로, 렌즈나 복잡한 광학계 없이, 작은 구멍(핀홀)을 통해 들어오는 빛만으로 이미지를 형성하였다. 이 원리는 이미 기원전 5세기경 중국과 그리스 철학자들이 언급했을 정도로 오래되었으며, 과학적으로는 아랍 학자 알하젠(Ibn al-Haytham)이 카메라 옵스큐라(Camera Obscura)의 원리를 정립하면서 발전하기 시작했다고 알려져 있다.
핀홀 카메라는 다음과 같은 원리로 작동한다.
- 어두운 상자에 아주 작은 구멍을 뚫는다.
- 외부의 빛은 이 구멍을 통과하며 직진 경로를 따라 내부 벽면(또는 필름)에 상을 맺는다.
- 이때 상은 좌우 및 상하가 반전된 형태로 나타난다.
렌즈가 없기 때문에 광학적 왜곡은 발생하지 않지만, 빛의 양이 극히 적게 들어오기 때문에 이미지가 어둡고 흐릿하며, 노출 시간이 길어져야 한다. 핀홀 카메라는 카메라의 광학 원리를 이해하기 위한 교육적 도구로 널리 사용되며, 오늘날에도 일부 예술 사진가들은 특유의 몽환적이고 부드러운 이미지를 위해 핀홀 카메라를 활용한다.
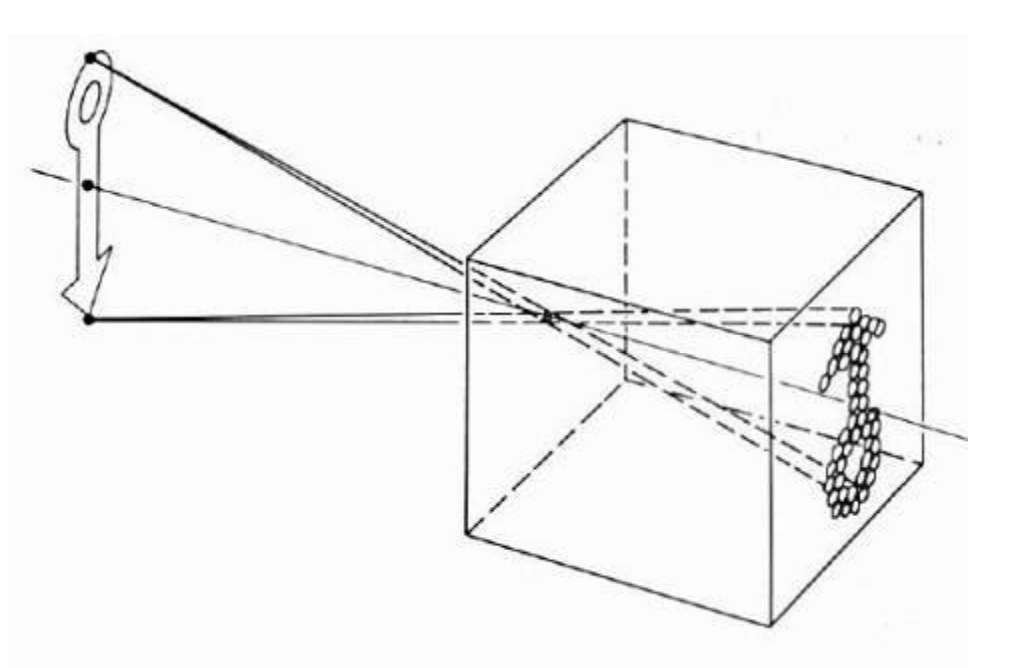
📐 Pinhole Camera Model
Figure 2: Pinhole 카메라 모식도
핀홀 카메라의 작동 원리는 기하광학적으로 간단하게 모델링할 수 있다. 빛은 항상 직선으로 진행하므로, 핀홀을 통과한 광선들은 하나의 점(핀홀 중심)을 기준으로 방사된다. 이 점을 투영 중심(Center of Projection, COP)이라 부르며, 이 COP에서 이미지 평면(Image Plane)까지의 거리를 초점 거리(focal length, \(f\))라고 정의한다.
\[f = \text{distance from COP to image plane}\]이 모델에서 중요한 점은, 모든 광선은 COP를 지나야 하며, 따라서 물체의 각 점은 COP를 통과한 직선 경로를 따라 이미지 평면에 정확히 투영된다. 이 때문에 렌즈를 사용하지 않더라도 정확한 상이 만들어질 수 있지만, 상의 밝기와 선명도는 제한된다.
🌫️ 왜 핀홀 카메라는 흐릿한가?
핀홀 카메라의 이미지는 선명하지 않고 흐릿하게 나타나는 경우가 많다. 그 이유는 크게 두 가지로 나뉜다.
핀홀의 크기 문제
핀홀이 너무 크면, 하나의 점에서 나오는 빛이 이미지 평면에 여러 경로로 도달하게 되어 상이 퍼져서 나타난다.
반대로 핀홀이 너무 작으면, 광선의 간섭 및 회절(Diffraction) 현상이 발생하여 역시 이미지가 흐려진다.회절(Diffraction) 효과
빛은 파동의 성질을 가지므로, 매우 작은 구멍을 통과할 때 회절 현상이 나타나 광선이 퍼지게 된다.
이로 인해 이론적으로 아무리 작은 핀홀을 뚫더라도 완벽하게 선명한 이미지를 얻을 수는 없다.
이러한 이유로, 핀홀 카메라의 화질에는 근본적인 한계가 존재하며, 이를 해결하기 위해 이후 카메라에는 렌즈와 조리개(Aperture)가 도입되었다.
🔘 Aperture: 조리개
Aperture(조리개)는 렌즈를 통과하는 빛의 양을 조절하는 장치로, 카메라에서는 조리개의 크기를 조절함으로써 노출량뿐만 아니라 초점 깊이(Depth of Field)에도 영향을 미친다.
📌 조리개가 작아지면
- 더 적은 양의 빛이 센서에 도달한다.
- 하지만 빛이 더 얇은 경로로 들어오기 때문에 이미지가 더 넓은 범위에서 선명하게 보인다 (심도가 깊어진다).
- 단점은 노출 시간이 길어져야 하므로 어두운 환경에서는 흔들림이 발생할 수 있다.
📌 조리개가 커지면
- 많은 양의 빛이 센서에 도달하므로 더 밝은 이미지를 얻을 수 있다.
- 그러나 특정 거리 이외의 물체는 흐릿해 보이게 된다 (심도가 얕아진다).
- 피사체를 강조하고 배경을 흐리게 만들고 싶을 때 유용하다.
앞서 설명한 것처럼, 너무 작은 조리개는 회절에 의한 선명도 저하를 초래할 수 있다. 따라서 실제 촬영에서는 단순히 조리개를 최대한 줄이는 것이 아니라, 화질과 심도 간의 균형을 고려한 적정 조리개 값(f-number)를 선택하는 것이 중요하다.
🔍 Thin Lens Model: 얇은 렌즈 모델
핀홀 카메라는 렌즈 없이도 이미지를 형성할 수 있지만, 빛의 양이 부족하고, 이미지가 흐릿하며, 노출 시간이 길다는 단점이 있다. 이를 해결하기 위해 광학 렌즈(lens)가 도입되었고, 그 구조를 수학적으로 단순화한 것이 바로 얇은 렌즈 모델(Thin Lens Model)이다. 얇은 렌즈는 렌즈의 두께가 거의 없다고 가정하며, 평행하게 입사한 빛을 한 점으로 모아주는 이상적인 렌즈로 설명된다.
📌 주요 개념
Figure 3: Thin Lens 모식도
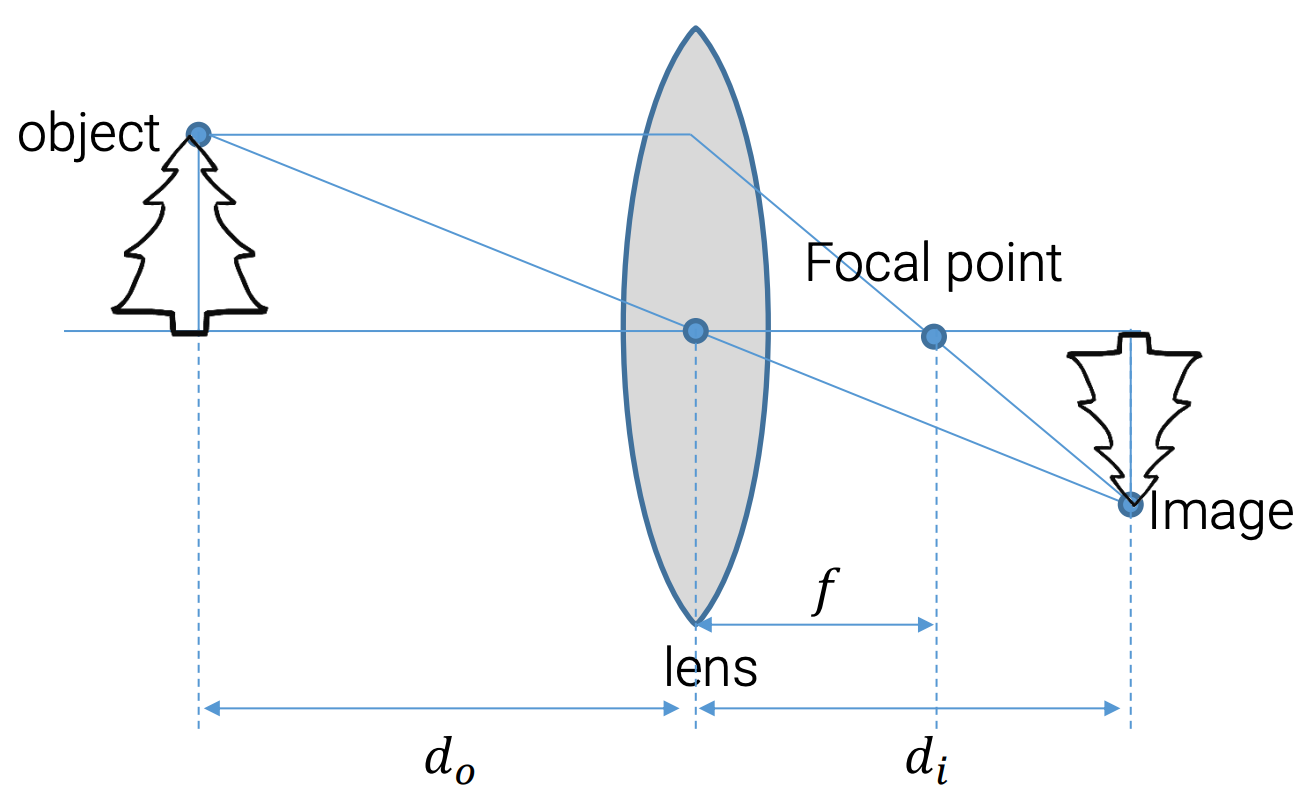
얇은 렌즈에서 물체와 이미지가 서로에 대해 정확히 초점이 맞을 조건은 다음 수식으로 표현된다.
\[\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}\]- Focal length (\(f\))
평행하게 입사하는 광선이 렌즈 뒤쪽 한 점에 모이는 거리를 말한다. 즉, 렌즈 중심에서 초점(focus)까지의 거리이다. - Object distance (\(d_o\))
물체가 렌즈 앞쪽에서 떨어진 거리 - Image distance (\(d_i\))
이미지가 맺히는 평면까지의 거리
이 식은 얇은 렌즈 방정식(thin lens equation)으로 불리며, 광학계에서 가장 기본이 되는 공식 중 하나이다.
🧮 Thin Lens Equation의 유도
\[\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}\]이 수식은 단순히 외워서 사용하는 것이 아니라, 기하학적 유추를 통해 직접 유도할 수 있다. 핵심 아이디어는 닮음 삼각형(similar triangles)과 확대율(Magnification)이다.
🔍 확대율 (Magnification Factor)
렌즈를 중심으로 물체와 상이 만들어지는 상황에서,
다음과 같은 두 쌍의 삼각형이 존재한다고 생각할 수 있다:
- 물체의 높이 \(h\)와 거리 \(d_o\)
- 이미지의 높이 \(h'\)와 거리 \(d_i\)
이를 통해 확대율 M을 정의할 수 있다:
\[M = \frac{h'}{h} = \frac{d_i}{d_o}\]이 비율은 두 삼각형의 대응변 길이의 비율과 같다.
또한 이 관계는 아래의 유사 삼각형 관계로부터 도출된다.
📐 닮음 삼각형을 통한 유도
다음은 얇은 렌즈를 통과하는 빛의 경로를 단면도로 본 상황이다:
- 물체로부터 온 광선은 렌즈 중심을 지나 직선으로 진행한다.
- 평행광선은 렌즈를 통과한 후 초점(\(f\))을 향해 굴절된다.
이때 두 삼각형의 대응관계는 다음과 같다:
- 물체에서 렌즈까지: 높이 \(h\), 거리 \(d_o\)
- 상에서 렌즈까지: 높이 \(h'\), 거리 \(d_i\)
첫 번째 삼각형 비율
\[\frac{h}{f} = \frac{h'}{d_i - f} \Rightarrow \frac{h'}{h} = \frac{d_i - f}{f}\]두 번째 확대율 정의
\[\frac{h'}{h} = \frac{d_i}{d_o}\]📌 식 정리 및 유도
두 식을 연결하면
\[\frac{d_i - f}{f} = \frac{d_i}{d_o}\]양변에 \(f, d_o\)를 곱하면
\[d_i d_o - f d_o = f d_i\]이를 정리하면
\[d_i d_o = f d_i + f d_o\]양변을 \(d_i, d_o\)로 나누면
\[1 = \frac{f}{d_o} + \frac{f}{d_i}\]따라서
\[\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}\]🎯 Focus와 Defocus
얇은 렌즈 방정식을 통해, 어떤 거리의 물체가 렌즈에 의해 어디에 초점을 맺는지를 계산할 수 있었다. 이제 이를 바탕으로 실제 이미지가 선명하게 맺히는 조건(= Focus)과 그렇지 않을 경우 흐릿해지는 현상(= Defocus)을 살펴보도록 하겠다.
🔍 Focus: 초점이 맞는 상태
얇은 렌즈 방정식을 만족할 때,
\[\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}\]이미지는 렌즈의 특정 거리 \(d_i\)에 정확히 맺히게 된다. 이때 이미지는 선명하고 또렷한 상으로 나타난다. 카메라에서는 이 조건을 만족시키기 위해 렌즈의 위치나 센서의 위치를 조절하게 된다.
🌫️ Defocus: 초점이 맞지 않는 상태
그러면 초점이 맞지 않는다는 것은 무슨 말일까? 바로 얇은 렌즈 방정식을 만족하지 않는다는 것이다.
\[\frac{1}{d_o} + \frac{1}{d_i} \ne \frac{1}{f}\]이미지는 한 점에 정확히 모이지 않게 되며, 센서 위에 퍼진 원 형태의 흐릿한 상이 형성되고, 이 퍼진 영역을 혼란 원(Circle of Confusion)이라고 부른다. 그럼 초점을 다시금 맞추기 위해서는 어떻게 할 수 있을까? 크게 2가지 방법이 있다.
- 렌즈를 앞뒤로 움직이기
- 대부분의 DSLR, Mirrorless 렌즈는 이 방식 사용
- \(d_i\)를 변화시켜 초점을 조절
- 센서를 움직이기 이 방법은 드물게 사용되며, 이를 통해 \(d_o\)에 따라 \(d_i\)를 조절하여 얇은 렌즈 방정식을 만족시키면 원하는 물체가 정확히 초점에 맞게 된다.
🌐 Field of View (FoV): 시야각
Field of View (FoV)란, 카메라가 한 번에 포착할 수 있는 장면의 범위를 의미한다. 즉, 이미지 안에 들어오는 실제 세계의 시야 각도를 수치화한 개념이다. 이는 렌즈의 초점 거리와 센서의 크기에 따라 결정된다.
🔭 Focal Length와 FoV의 관계
렌즈의 초점 거리(\(f\))가 짧을수록 더 넓은 범위를 촬영할 수 있고 (광각), 반대로 초점 거리가 길수록 시야는 좁아지고 줌인된 이미지가 만들어진다.
- 짧은 초점 거리 → 넓은 FoV → 더 많은 장면을 한 프레임에 담음
- 긴 초점 거리 → 좁은 FoV → 먼 물체를 확대하는 효과
📐 Sensor Size와 FoV의 관계
센서의 크기 또한 FoV에 중요한 영향을 미친다. 같은 렌즈를 사용할 때
- 센서가 클수록 더 넓은 영역이 촬영된다.
- 센서가 작을수록 중심 영역만 잘려 나와 크롭(crop) 효과가 발생한다.
즉, 센서가 작아질수록 동일한 초점 거리에서도 FoV는 줄어들게 된다.
📏 수식으로 표현하는 FoV
입사 광선이 평행하며 물체가 무한대에 있다고 가정하면, FoV는 다음과 같은 삼각함수 관계로 유도할 수 있다.
\[FOV = 2 \cdot \tan^{-1} \left( \frac{h}{2f} \right)\]- \(h\): 센서의 높이 (또는 대각선/너비로 대체 가능)
- \(f\): 초점 거리
이 공식은 광선이 평행(= 물체가 무한대에 위치)일 때 성립한다. 즉, 이미지 평면이 렌즈의 초점 거리 위치(\(d_i = f\))에 놓여야 한다.
🎯 FoV 유지하며 피사체 크기 유지하기 & 셀카 왜곡 현상
Figure 4: 초점거리에 따른 셀카 왜곡 현상
같은 피사체를 같은 크기로 담고 싶다면, 초점 거리가 짧을수록 카메라는 더 가까이 접근해야 하고, 초점 거리가 길수록 더 멀리 떨어져야 한다. 하지만 이 과정에서 단순히 피사체 크기만 동일한 것이 아니라, 배경이 포함되는 방식과 왜곡 정도는 매우 달라진다. 짧은 초점 거리(광각) + 가까이 접근하여 촬영하게 되면 배경이 왜곡되고 넓게 펼쳐지게 되며, 긴 초점 거리(망원) + 멀리서 촬영한 경우에도 동일하게 피사체의 크기가 나타나지만 배경이 압축되어 좁게 보이게 된다. 즉, 초점 거리가 다르면 피사체 주변 공간의 인상 자체가 달라진다.
이걸 확장해서 우리가 흔하게 사용하는 스마트폰을 이용해서 셀카를 찍는 경우를 생각해보자. 우리가 스마트폰 셀카 카메라에서 자주 발생하는 문제는 바로 광각 렌즈에 의한 얼굴 왜곡으로, 이는 스마트폰 전면 카메라가 일반적으로 24~28mm 광각 렌즈를 사용하기 때문이다. 우리는 셀카를 찍을 때 팔 길이만큼만 손을 뻗을 수 있기에 카메라와 매우 가까운 상태이고 이로 인해 코나 이마는 과장되어 크고, 귀나 얼굴 가장자리는 눌려 보이는 배럴 왜곡(barrel distortion)이 발생하게 되는 것이다. 이러한 왜곡은 초점 거리와 촬영 거리의 조합으로 인한 광학적 원근 왜곡이며, 같은 얼굴을 망원 렌즈로 멀리서 찍으면 더 자연스럽게 보인다.
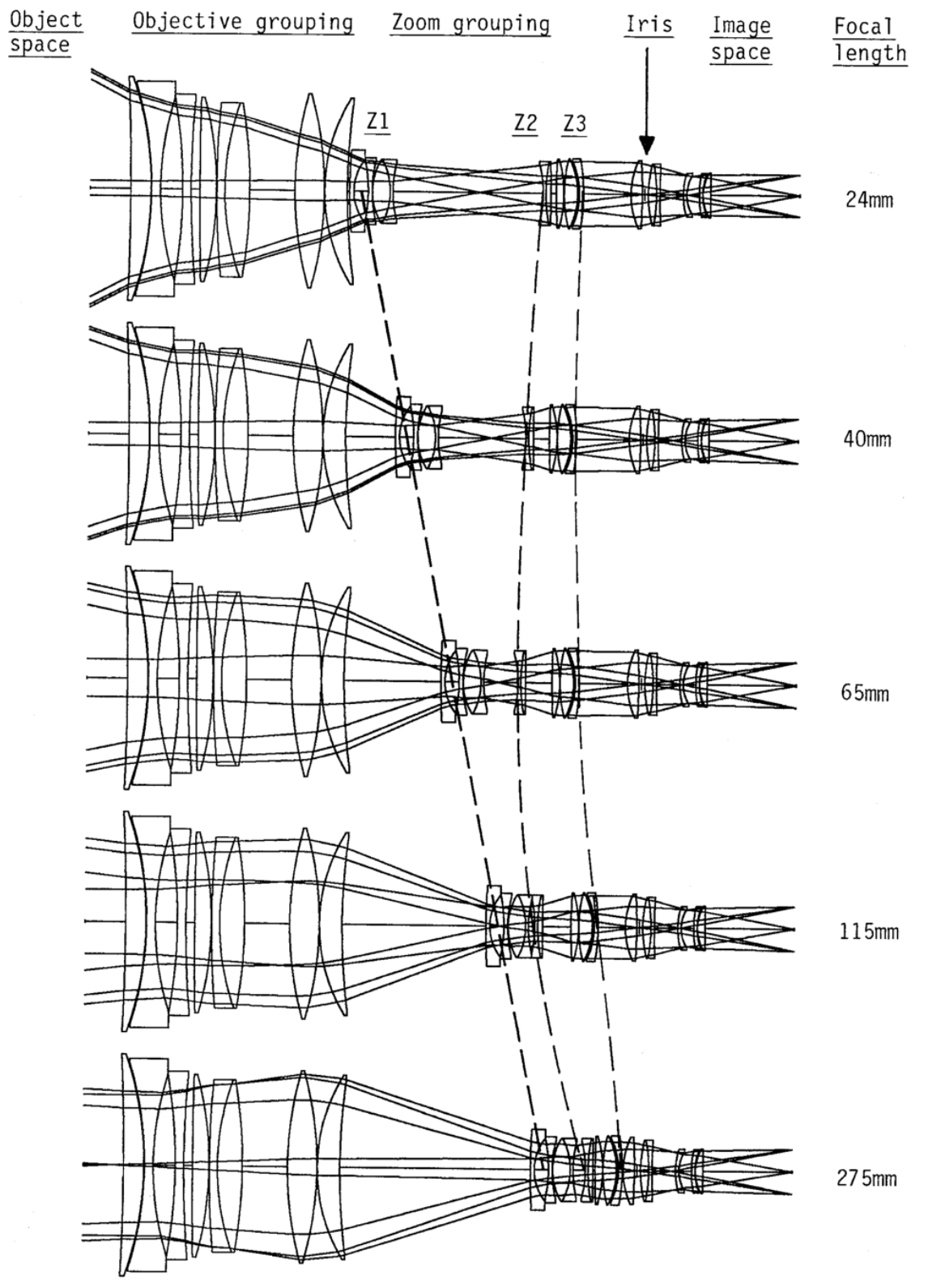
🔧 Zoom Lens: 초점 거리를 바꿀 수 있는 렌즈
Figure 5: Zoom Lens 모식도
줌 렌즈는 여러 개의 렌즈 요소를 포함하고 있으며, 렌즈 그룹 간의 상대적 위치를 조절함으로써 초점 거리를 변화시키게 된다. 즉, 카메라를 움직이지 않고도 시야각(FoV)을 조절할 수 있다는 것을 의미한다. NIKON Coolpix P1000의 경우에는 125배 광학 줌을 지원하는 카메라인데 이의 초점거리 범위가 4.3mm – 539mm로 매우 광범위하다며, 이로 인해 200m 떨어진 간판의 글씨부터 5km 떨어진 건물까지도 읽을 수 있을 정도로 강력한 줌 기능을 제공한다고 알려져 있다.
🌕 Depth of Field (DoF): 심도
Depth of Field (DoF, 심도)란, 사진에서 초점이 맞아 보이는 거리의 앞뒤 범위를 의미한다. 즉, 이미지 내에서 선명하게 보이는 피사체가 위치할 수 있는 거리의 폭을 말하며 얕은 심도(Shallow DoF)란 것은 특정 거리만 선명, 나머지는 흐릿한 경우를 의미하며, 반대로 깊은 심도(Deep DoF): 앞뒤로 넓은 범위가 선명하게 보이는 경우를 말한다. 얕은 심도는 배경히 흐릿하고 피사체만 뚜렷해야하는 인물 촬영에 적합하고, 풍경사진을 찍을 때는 깊은 심도로 촬영하는 것이 적합하다. 이와 함께 나오는 개념이 Circle of Confusion이다. 이는 초점이 맞지 않는 물체에 나타나는 현상으로 센서에 점이 아닌 퍼진 원 형태로 나타나게 된다. 이 원을 Circle of Confusion이라고 하며, 이 크기가 작으면 이는 곧 이미지가 선명하다는 것을 의미한다. DoF는 이 원의 크기가 허용 가능한 범위 내일 때로 정의하게 된다.
그럼 이런 심도, Depth of Field에 영향을 주는 요인에는 무엇이 있을까?
🔧 심도에 영향을 주는 요인
- 조리개(Aperture, f-number)
- 조리개를 좁게 열수록 (f-number ↑) → 심도 깊어짐
- 조리개를 넓게 열수록 (f-number ↓) → 심도 얕아짐
- 초점 거리(Focal length)
- 초점 거리가 길수록 → 심도가 얕아짐
- 초점 거리가 짧을수록 → 심도가 깊어짐
- 피사체 거리(Object distance)
- 카메라에 가까울수록 → 심도가 얕아짐
- 멀어질수록 → 심도가 깊어짐
💡 Exposure: 노출
Figure 6: 노출을 짧게 조절하였을 때 촬영된 사진 예시
사진을 촬영할 때, 가장 중요한 기본 요소 중 하나는 노출(Exposure)이다. 노출은 말 그대로 센서가 얼마나 많은 빛을 받아들이는가를 의미하며, 결국 이미지의 밝기를 결정하는 핵심 요인이다. 적절한 노출이 되면 사진은 밝기, 명암, 색감이 균형 있게 담기지만, 빛이 너무 적으면 어두운 사진(underexposed), 너무 많으면 하얗게 날아간 사진(overexposed)이 된다.
그럼 이러한 노출은 어떤 변수에 영향을 받게 될까? 크게 3가지로 생각해볼 수 있다.
- 셔터 속도 (Shutter Speed)
- 조리개 (Aperture, f-number)
- ISO 감도 (Sensor sensitivity)
이 세 가지는 서로 영향을 주고받으며, 이들의 관계는 노출 삼각형(Exposure Triangle)이라는 개념으로 시각화된다. 그 전에 ISO가 무엇인지부터 짚고 넘어가도록 하겠다.
🎚️ ISO 감도 (Sensor Sensitivity)
디지털 카메라에서 ISO는 센서가 빛에 얼마나 민감하게 반응하는지를 수치로 표현한 값으로, 이는 자동으로 설정되기도 하고, 수동으로 조절할 수도 있다. ISO 값은 일반적으로 다음과 같이 두 배씩 증가하는 형태를 갖게 되며 이러한 변화는 선형적 관계를 가지며, 예를 들어 ISO 200은 ISO 100보다 절반의 빛만으로도 동일한 노출을 낼 수 있다는 의미다.
\[\text{ISO} \in \{100, 200, 400, 800, 1600, 3200, 6400, \dots\}\]💡 ISO 값이 낮을 때
- 빛에 덜 민감하다 → 더 많은 빛이 필요하다.
- 장점: 이미지 품질이 우수, 노이즈가 거의 없음
- 단점: 실내나 야간 촬영 등 빛이 부족한 환경에서는 노출 확보가 어려움
💡 ISO 값이 높을 때
- 빛에 더 민감하다 → 적은 빛으로도 촬영 가능
- 장점: 어두운 환경에서 노출 확보 가능
- 단점: 노이즈 증가, 색상 왜곡 및 디테일 손실
Exposure Triangle
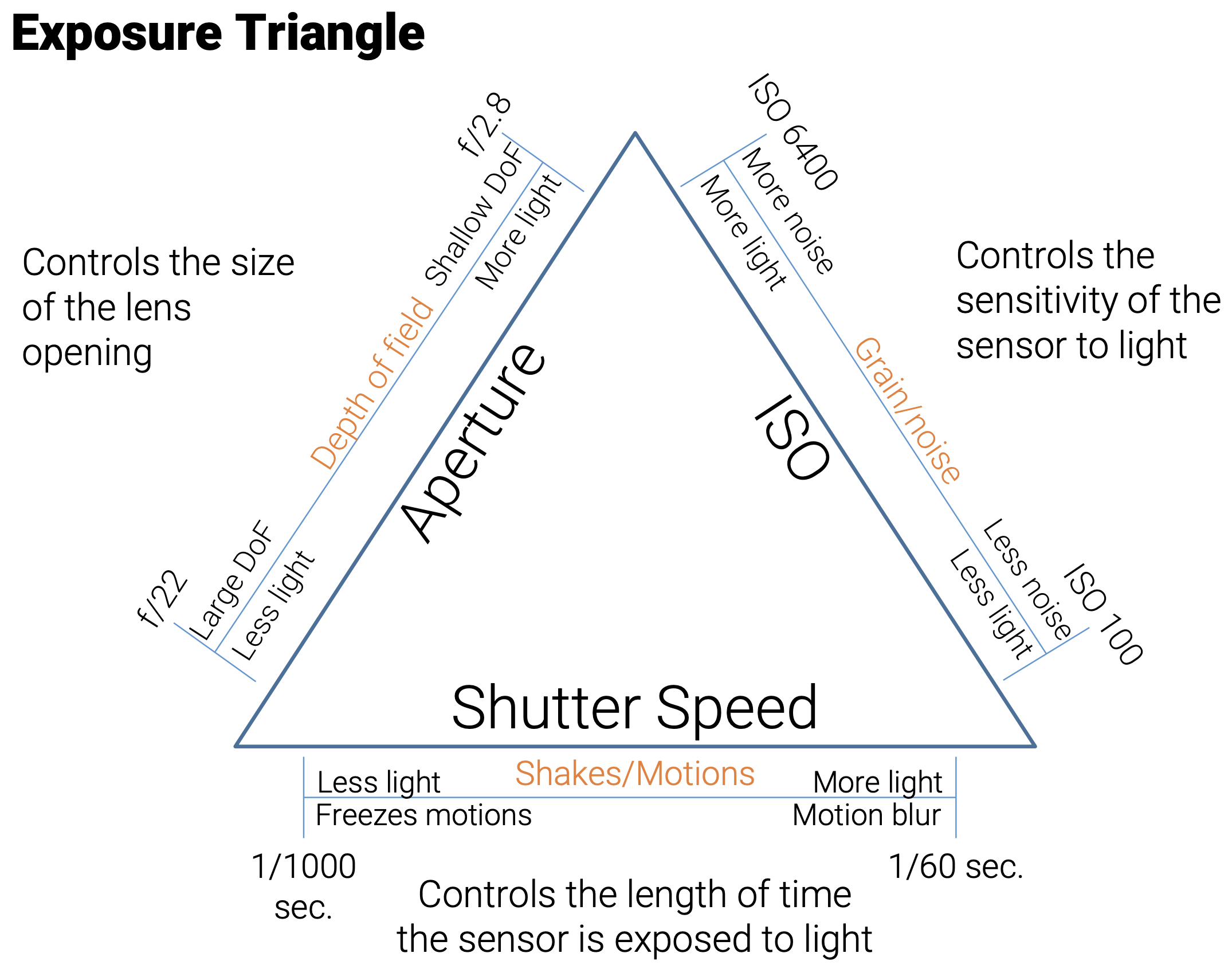Figure 7: Exposure Triangle 모식도
노출 삼각형은 노출을 조절하는 세 가지 요소의 균형 관계를 보여준다. 이 세 축 중 하나를 조절하면, 나머지 둘을 조정해 동일한 노출값을 유지할 수 있다.
| 요소 | 설명 | 영향 |
|---|---|---|
| ⏱️ 셔터 속도 | 센서가 빛에 노출되는 시간 | 길수록 밝고, 짧을수록 어두움 |
| 🔘 조리개 | 렌즈가 빛을 통과시키는 구멍의 크기 | 클수록 밝고, 작을수록 어두움 |
| 🌙 ISO 감도 | 센서의 빛에 대한 민감도 | 높을수록 밝지만 노이즈 증가 |
다시금 각각의 요소를 간단히 정리해보도록 하겠다.
⏱️ 셔터 속도 (Shutter Speed)
셔터 속도는 센서가 열려서 빛을 받아들이는 시간을 말한다.
- 짧은 셔터 속도 (예: 1/1000초):
- 빠르게 움직이는 피사체도 정지된 듯 담을 수 있음
- 빛이 적게 들어와 어두워질 수 있음
- 긴 셔터 속도 (예: 1초):
- 야경 촬영, 별빛이나 물의 흐름을 부드럽게 표현
- 손떨림이나 움직임으로 인해 흔들림 발생 가능
- 삼각대 필요
| 셔터 속도 | 특징 |
|---|---|
| 1/1000초 | 움직임 정지, 어두움 |
| 1/60초 | 일반 촬영 기준 |
| 1초 이상 | 야경, 별 궤적, 흔들림 주의 필요 |
🔘 조리개 (Aperture, f-number)
조리개는 렌즈 내부의 빛이 통과하는 구멍의 크기를 조절하는 장치라는걸 앞서 확인하였다. 이는 f-number로 표현되며, 숫자가 작을수록 더 넓게 열림, 클수록 좁게 조여짐을 뜻한다. 그리고 우리가 앞서 살펴보았듯이 조리개는 단순히 밝기뿐 아니라, 심도(Depth of Field)에도 영향을 준다는 것도 까먹지 않아야 한다.
| f-number | 조리개 크기 | 심도 |
|---|---|---|
| f/1.4 | 매우 넓음 | 얕은 심도 (배경 흐림) |
| f/8 | 중간 | 적절한 심도 |
| f/16 | 매우 좁음 | 깊은 심도 (전체 선명) |
🌙 ISO 감도
ISO는 센서가 빛에 얼마나 민감하게 반응할 것인가를 결정하는 수치다.
- 낮은 ISO(100~200)
- 깨끗하고 선명한 이미지
- 빛이 충분할 때 사용
- 높은 ISO(1600 이상)
- 어두운 환경에서도 밝게 촬영 가능
- 하지만 노이즈 증가로 이미지 품질 저하
| ISO 값 | 특징 |
|---|---|
| 100 | 낮은 감도, 낮은 노이즈, 밝기 낮음 |
| 800 | 중간 감도, 실내 적당 |
| 3200 | 고감도, 어두운 환경 적합, 노이즈 있음 |
⚖️ 노출 균형의 실제 적용
노출 삼각형에서 하나의 축을 바꾸면 나머지 둘로 균형을 맞춰야 한다.
예시 1:
- 조리개를 f/4 → f/8로 조임 (어두워짐)
→ 셔터 속도를 더 길게 하거나, ISO를 더 높여 보정
예시 2:
- 셔터 속도를 1/1000초로 빠르게 함 (어두워짐)
→ 조리개를 열거나, ISO를 높여야 적정 노출 유지 가능
📉 Lens Flaws: Chromatic Aberration (색수차)
Figure 8: 색수차 예시
렌즈를 통해 빛이 굴절될 때, 모든 파장(색)의 빛이 동일한 위치에 정확히 초점을 맺지 않는 현상을 색수차(Chromatic Aberration)라고 한다. 이는 렌즈 재질의 굴절률이 빛의 파장에 따라 다르기 때문에 발생하며, 결과적으로 이미지의 경계 부분에서 색 번짐 현상이 나타난다. 이는 어떻게 발생하게 되는 것일까? 백색광(white light)은 다양한 파장의 빛으로 구성되어 있으며, 렌즈를 통과할 때 다음과 같은 현상이 발생한다.
- 짧은 파장 (보라색, 파란색) → 굴절률이 높아 더 많이 굴절됨
- 긴 파장 (빨간색) → 굴절률이 낮아 덜 굴절됨
이로 인해 동일한 물체의 이미지가 서로 다른 위치에 맺히게 되며, 특히 고대비 경계 부분에서 다음과 같은 색상 왜곡이 발생한다. 경계 주변에 보라색, 파란색, 초록색, 빨간색 띠가 생기게 된다.
🛠️ 어떻게 보정할 수 있을까?
- 광학적 설계 보정
- Achromatic Lens (아크로매틱 렌즈): 서로 다른 재질의 렌즈를 조합해 두 가지 파장을 동일한 초점에 맺히도록 설계
- Apochromatic Lens (아포크로매틱 렌즈): 세 가지 이상의 파장을 보정해 더욱 정밀한 색수차 감소
- 디지털 후처리 보정
- 이미지 프로세싱 소프트웨어에서 자동으로 색 번짐을 감지하고 제거
- Lightroom, Photoshop 등에서 Chromatic Aberration 제거 기능이 일반적으로 제공됨